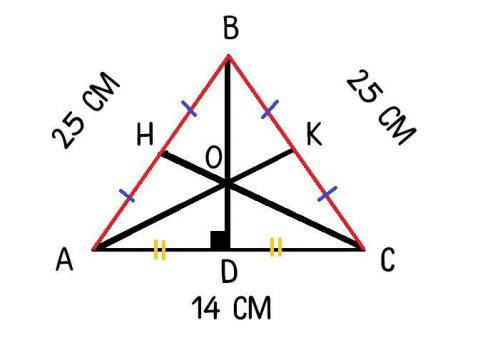
Рассмотрим ΔABC - равнобедренный; AB=BC=25 см;
BD - медиана ⇒ AD=DC=14:2=7 см
Т.к. ΔABC - равнобедренный, то BD - является и высотой, и биссектрисой еще.
Рассмотрим ΔABD - прямоугольной; ∠D - прямой, AB=25см; AD=7 см
по т. Пифагора найдем BD
BD² = AB² - AD²
BD² = 25² - 7²
BD = 24 cм
Рассмотрим еще раз ΔABC:
по свойству медианы OD=1/3 * BD = 1/3 * 24 = 24 : 3 = 8 см
Рассмотрим ΔCOD - прямоугольный; ∠D - прямой; DC=7 см; OD=8 см
по т.Пифагора найдем OC
OC² = OD² + DC²
OC² = 8² + 7²
OC = 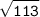 см
см
по свойству медианы 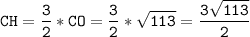 см
см
по свойству равнобедренного треугольника CH=AK= 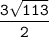 см
см
ответ: 24 см; 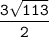 см;
см; 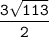 см
см
пусть ВС = х см, тогда АД 3х, так как средня линия равна полусумме оснований (пусть средня линия это МЕ), то МЕ = 2х...следовательно АВ = 2х..Проведём высоту ВН и СН1, тругольники АВН и Н1СД равны, значит АН = Н1Д..ВС = НН1, так как НВСН1 - прямоугольник, значит НН1 = х, а АН + Н1Д=2х, то есть АН и Н1Д =х..через косинус угла А найдём сам угл..cos A = x/2x=1/2 следовательно угол А равен 60