Площадь прямоугольного треугольника равна половине произведения катетов. Один катет 5 , другой можем найти. По правилу, катет, лежащий против угла 30 градусов равен половине гепотенузы. Т. е. АС=6. Теперь можем найти площадь: (5*6):2=15
Доказательство. Рассмотрим треугольник ABC с высотами AA1, BB1 и CC1 и докажем, что прямые AA1, BB1 и CC1 пересекаются в одной точке.
Проведем через точки A, B, C прямые, соответственно перпендикулярные к прямым AA1, BB1, CC1 и, следовательно, соответственно параллельные прямым BC, CA, AB (рис. 79). Эти прямые, пересекаясь, образуют треугольник A2B2C2.
Так как C2A || BC и C2B || AC, то четырехугольник BC2AC — параллелограмм, поэтому C2A = BC. По аналогичной причине AB2 = BC. Из этих двух равенств следует, что C2A = AB2, т. е. точка A — середина отрезка C2B2. Аналогично можно доказать, что точки B и C — середины отрезков A2C2 и A2B2.
Таким образом, прямые AA1, BB1, CC1 являются серединными перпендикулярами к сторонам треугольника A2B2C2, поэтому они пересекаются в одной точке. Теорема доказана.
Точку пересечения высот треугольника (или их продолжений) для краткости называют ортоцентром треугольника.
Итак, с каждым треугольником связаны четыре точки: точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам, точка пересечения медиан и ортоцентр. Эти четыре точки называются замечательными точками треугольника.
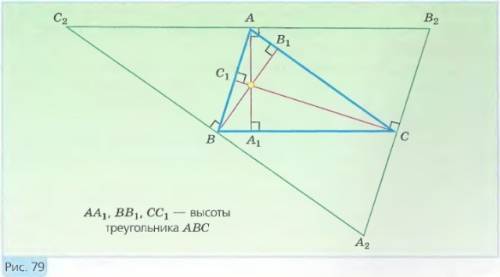
Доказательство. Рассмотрим треугольник ABC с высотами AA1, BB1 и CC1 и докажем, что прямые AA1, BB1 и CC1 пересекаются в одной точке.
Проведем через точки A, B, C прямые, соответственно перпендикулярные к прямым AA1, BB1, CC1 и, следовательно, соответственно параллельные прямым BC, CA, AB (рис. 79). Эти прямые, пересекаясь, образуют треугольник A2B2C2.
Так как C2A || BC и C2B || AC, то четырехугольник BC2AC — параллелограмм, поэтому C2A = BC. По аналогичной причине AB2 = BC. Из этих двух равенств следует, что C2A = AB2, т. е. точка A — середина отрезка C2B2. Аналогично можно доказать, что точки B и C — середины отрезков A2C2 и A2B2.
Таким образом, прямые AA1, BB1, CC1 являются серединными перпендикулярами к сторонам треугольника A2B2C2, поэтому они пересекаются в одной точке. Теорема доказана.
Точку пересечения высот треугольника (или их продолжений) для краткости называют ортоцентром треугольника.
Итак, с каждым треугольником связаны четыре точки: точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам, точка пересечения медиан и ортоцентр. Эти четыре точки называются замечательными точками треугольника.

т.к. угол В = 30 градусов,то АС=1/2*АВ=1/2*12=6см
Площадь треугольника=1/2*ВС*АС=1/2*5*6=15 кв.см
ответ:15 кв.см