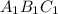- его проекция на плоскость P. 
.
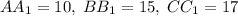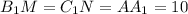дм. Тогда BM = 15-10 = 5 дм, CM = 17-10 = 10 дм.
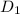. Этот перпендикуляр разделит отрезок NM пополам. Значит 
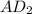медиана треугольника 
.
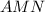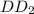- средняя линия трапеции BCNM. Его длина 
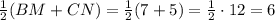дм.
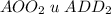подобны по первому признаку: 
- общий, 
.
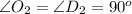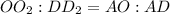
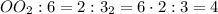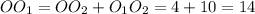дм.
дм.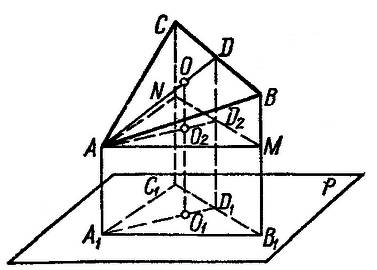
1)∠ABC = ∠BCD = 35°как накрест лежащие при пересечении АВ║CD секущей ВС.
2)∠ABC = ∠АСВ = 35° как углы при основании равнобедренного треугольника.
3)∠ACD = ∠АСВ + ∠BCD = 35° + 35° = 70°
4)∠САВ = 180° - ∠ACD = 180° - 70° = 110° так как эти углы - односторонние при пересечении АВ║CD секущей АС