Площадь боковой поверхности равна 756 дм².
Площадь полной поверхности равна 1145 дм².
Объяснение:
Площадь боковой стороны усеченной пирамиды равна площади равнобочной трапеции с основаниями 17 и 10 дм и высотой, равной апофеме 14 дм.
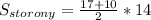
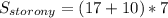
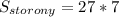
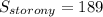 дм².
дм².
В площади боковой стороны таких трапеций четыре.
Значит
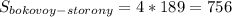 дм².
дм².
Площадь полной поверхности равна сумме площади боковой поверхности и площадей оснований.
Площадь меньшего основания равна площади квадрата со стороной 10 дм
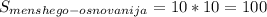 дм².
дм².
Площадь большего основания равна площади квадрата со стороной 17 дм
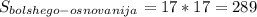 дм².
дм².
Теперь надо сложить все эти три площади
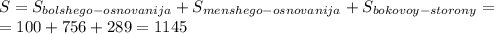
дм².
Объяснение:
Определение
Геометрическим местом точек (сокращенно — ГМТ), обладающих некоторым свойством, называется множество всех точек, которые обладают этим свойством.
Решение задачи на поиск ГМТ должно содержать доказательство того, что все точки множества , указанного в ответе, обладают требуемым свойством, а также наоборот, что все точки, обладающие требуемым свойством, лежат в этом множестве .
Приведем классические и важнейшие известные примеры ГМТ.
Пример
Геометрическое место точек, удаленных от данной точки на заданное положительное расстояние, — окружность (это определение окружности).
Пример
Геометрическое место точек, равноудаленных от данной прямой, — две параллельные прямые.
Пример
Геометрическое место точек, равноудаленных от концов отрезка, — серединный перпендикуляр к отрезку.
Пример
Геометрическое место внутренних точек угла, равноудаленных от его сторон, — биссектриса угла.
Два последних примера будут рассмотрены детально в разделах "Серединный перпендикуляр" и "Биссектриса".
Утверждение
ГМТ, обладающих двумя свойствами, является пересечением двух множеств: ГМТ, обладающих первым свойством, и ГМТ, обладающих, вторых свойств
Хе
Объяснение:
Не знаю