
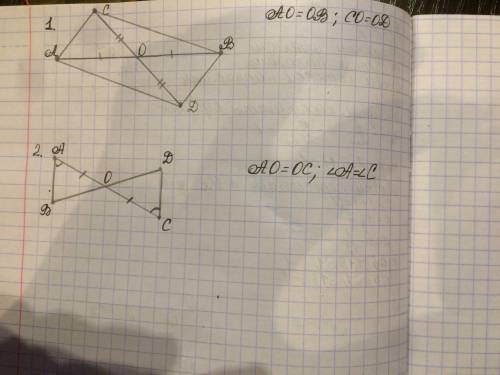
1. а) Наклонные КА,КВ,КС и КD равны (дано), значит равны и их проекции на плоскость АВСD. Следовательно, АО=ВО=СО=DO => точка О - точка пересечения диагоналей квадрата, то есть его центр. Что и требовалось доказать.
б) По Пифагору АС=√(AD²+DC²) = √144 =12. ОС = 6.
КО=√(КС²-ОC²) = √(100-36) = 8.
2. Проекция точки М на плоскость АВС - центр О вписанной в треугольник АВС окружности, так как проекции равных наклонных равны. Радиус вписанной окружности найдем по формуле: r = S/p, где S - площадь треугольника, а р - его полупериметр. У нас р = (3√2+3√2+2√2)/2 = 4√2.
По формуле Герона S = √(p*(p-a)(p-b)(p-c). У нас
S= √(4√2*√2*√2*2√2) = 4√2. Тогда r = 4√2/4√2 = 1.
В прямоугольном треугольнике СОН катет ОН=1, катет СН=АС/2 = √2. Тогда по Пифагору ОС = √(1+2) = √3.
Тангенс угла МСО (а это и есть искомый угол, так как угол между наклонной прямой и плоскостью равен углу между этой наклонной и ее проекцией на плоскость) равен отношению противолежащего катета к прилежащему:
МО/ОС = 1/√3. А это угол, равный 60°.
ответ: угол наклона прямой МС к плоскости треугольника равен 60°

А4. 4 120°
А5. 1 10
A6. 1 16
A7. 2 6√5
А4. Угол тупой: значит 150° или 120°
S=1/2 AB*AC sin α;
3√3=1/2 *6*2sin α;
sinα=√3/2; α=120°
A5.
Если известно две стороны треугольника и угол между ними, то площадь данного треугольника вычисляется, как половина произведения этих сторон умноженная на синус угла между ними.
угол тупой sin 150=1/2
значит α=120
или 3√3=6*2sinα/2→sinα=√3/2, α=120°
А5.
Высота, проведенная к основанию, делит его на две равные части, и косинус искомого угла становится равен половине основания, деленного на боковую сторону: cosα=b/(2a), где а- боковые стороны
√0,91=2√91/2а; а=√91/√0,91=10
A6. S=pr, де р=Р/2
A7. Когда известны стороны ищем площадь по формуле Герона
Найдём полупериметр
р=(4+7+9)/2=10
Если ты сама не напишешь дано , найти и ответ к каждой задаче- то больше не буду! Да, и формулу Герона найди и выпиши перед решением