
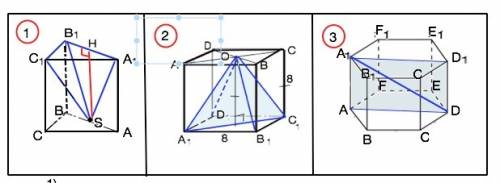
1)
Т.к. призма прямая, её грани перпендикулярны основаниям.
Грань SA1B1 пирамиды лежит в плоскости АВВ1А1, высота SH перпендикулярна основанию А1В1С1 и параллельна боковому ребру призмы, следовательно, её длина равна длине ребра АА1.
2)
Пусть АВСD - верхнее основание куба, а нижнее A1B1C1D1.
Диагонали основания пирамиды OA1B1C1D1 совпадают с диагоналями квадрата А1В1С1D1, высота ОН равна расстоянию между параллельными основаниями куба, т.е. длине его ребер - 8 дм.
Диагональное сечение пирамиды - треугольник А1ОС1. Основание А1С1 - диагональ квадрата со стороной А1В1=8. А1С1=8√2 (как диагональ квадрата).
S(A1OC1)=OH•A1C1:2=8•8√2*2=32√2 дм²
3)
В этой задаче допущена неточность. Длины ребер правильной шестиугольной призмы равны.
В основании этой призмы правильный шестиугольник, а все 6 граней - квадраты. Площадь каждого 96:6=16 см²
Тогда ребро призмы √16=4 см.
Правильный шестиугольник можно разделить на 6 правильных треугольников, и длина бóльшей его диагонали равна длине 2-х ребер.
На рисунке приложения АD и А1D1 - бóльшие диагонали оснований, а А1D - бóльшая диагональ призмы.
По т.Пифагора
А1D=√(AA1²+AD²)=√(4²+8²)=4√5
Гульсарочка как то вокруг решения ходит :) Диагонали у параллелограмма не равны, только у прямоугольника.
Вот как можно поступить. Берется прямоугольный треугольник со стронами 5,12,13. На катете 12 от вершины прямого угла откладывается отрезок, равный малому катету, то есть 5, и соединяется с противоположной вершиной треугольника. Получился треугольник со сторонами 12 - 5 = 7, 13 и 5*корень(2).
Вот на такие два треугольника и делит заданный параллелограмм диагональ длинны 13. Можно легко достроить его, проведя 2 линии, параллельные сторонам этого треугольника, через противоположные вершины.
Площадь такого параллелограмма равна 5*7 = 35.
Вот какая штука. В моем решении (и - между прочим, в решении Гульсарочки!) вторая сторона параллелограмма получается 5*корень(2), что больше 7 (совсем немного, но - больше). Поэтому вторая высота (проведенная к этой стороне) - меньше 5 (произведение высоты на сторону равно площади). Поэтому мое решение не соответствует условию, в котором сказано, что 13 - наибольшая из диагоналей, а 5 - наименьшая из высот.
В решении же Гульсарочки, которое получается, если от вершины прямого угла откладывается отрезок, равный 5, вдоль продолжения катета 12, то есть длина стороны параллелограмма равна 12 + 5 =17. Это решение ничем не хуже и не лучше моего, поскольку тоже не удовлетворяет всему условию :) - в этом случае диагональ 13 не наибольшая.