
Все грани прямоугольного параллелепипеда - прямоугольники.
Двугранный угол DABD₁ - это угол между плоскостями DAB и ABD₁.
АВ - ребро двугранного угла.
DA⊥AB как стороны квадрата,
DA - проекция наклонной D₁A на плоскость DAB, значит
D₁A⊥АВ по теореме о трех перпендикулярах.
DA⊥AB и D₁A⊥АВ,, значит ∠D₁AD - линейный угол двугранного угла D₁ABD.
ΔADC: ∠ADC = 90°, по теореме Пифагора
AD = √(AC² - CD²) = √(100 - 36) = √64 = 8 дм
ΔD₁AD: ∠D₁DA = 90°, DD₁ = AA₁ = 8√3 дм, AD = 8 дм,
tg∠D₁AD = D₁D / AD = 8√3 / 8 = √3
∠D₁AD = 60°
Дано :
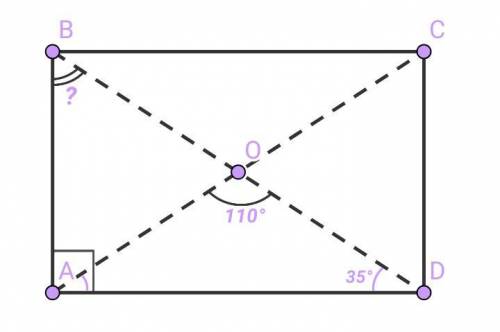
Четырёхугольник ABCD —прямоугольник.
Отрезки АС и BD — диагонали.
Точка О — точка пересечения диагоналей.
Угол AOD = 110°.
Найти :
Угол ABD = ?
Рассмотрим треугольник AOD.
Диагонали прямоугольника точкой пересечения делятся пополам и равны.
Следовательно —
АО = OD.
Тогда треугольник AOD — равнобедренный.
У равнобедренного треугольника углы у основания равны.
Следовательно —
Угол OAD = угол ODA.
По теореме о сумме углов треугольника —
Угол ODA = 0,5*(180° - угол AOD) = 0,5*(180° - 110°) = 0,5*70° = 35°.
Рассмотрим треугольник BAD — прямоугольный (так как угол BAD = 90° по определению прямоугольника).
Сумма острых углов прямоугольного треугольника равна 90°.
Следовательно —
Угол ABD = 90° - угол BDA
Угол ABD = 90° - 35° = 55°.
55°.
угол АОС = угол АОВ+ВОС
ФОЕ=ВОС как вертикальные значить угол АОС=20°+70°=90°