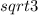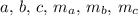 - длины сторон и медиан треугольника ABC,
- длины сторон и медиан треугольника ABC, 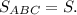 Воспользовавшись формулу
Воспользовавшись формулу 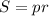 и то, что
и то, что 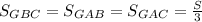 , получаем, что нужно доказать неравенство.
, получаем, что нужно доказать неравенство.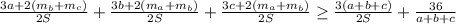
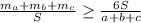
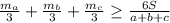
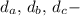 расстояния от точки G к сторонам a, b, c треугольника АВС. Очевидно, что
расстояния от точки G к сторонам a, b, c треугольника АВС. Очевидно, что 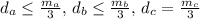 Также имеем
Также имеем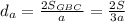 . Аналогично,
. Аналогично, 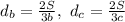
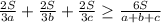 , которое равносильна неравенству, что выражает отношение между средним арифметическим и средним гармоническим 3 положительных чисел:
, которое равносильна неравенству, что выражает отношение между средним арифметическим и средним гармоническим 3 положительных чисел: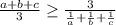
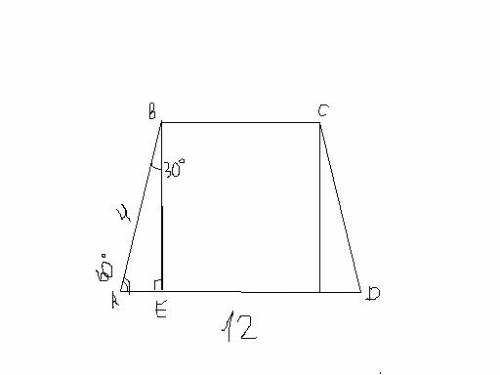
5.угол ВАЕ =60 град, значит угол АВЕ=30град.в прямоуг треуг против угола 30 градусов лежит сторона равная половине гипотенузы, значит половине боковой стороны с длиной 4 , то есть АЕ=2, СООТВЕТСТВЕННО ЧТОБ ПОЛУЧИЛСЯ ВЕРХ ТРАПЕЦИИ ,Надо из низа (12) вычесть два таких симметричных отрезка 12-2-2=8.
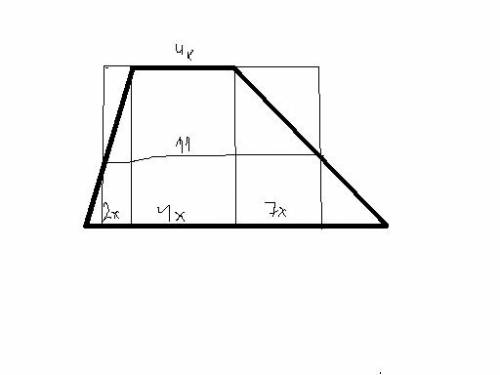
6. площадь трапеции равна произведению ее сред линии на высоту h,но также произведению среднего арифметического оснований на эту же высоту.Высоту сокращаем и приравниваем 11=((2х+4х+7х это низ) +4х (это верх))/2 .....х=11/17, 4х(верх)=44/17 (сократишь сам),низ =2х+4х+7х=13х=13*11/17= ...сам дорешаешь.
Т.к. пирамида правильная, значит в основании лежит равносторонний треугольник АВС, в котором высота является и медианой и биссектрисой. Точкой Р обозначим точку, в которую опущена высота ВР этого треугольника. Высота делит АВС на два равных прямоугольных треугольника АВР и ВРС.
Пусть АВ=х - сторона основания пирамиды, тогда РС=х/2.
Тогда по теореме Пифагора х^2=(x/2)^2+3^2
или x^2=1/4*x^2+9. Отсюда находим х=корень из 12.
Тогда площадь равностороннего треугольника Sabc=1/2*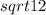 *
*![sqrt{12}[/tex*sin60=3[tex]sqrt{3}](/tpl/images/0167/6314/05f01.png)
Периметр треугольника Р=3*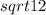
Тогда площадь полной поверхности пирамиды есть S=1/2PL+Sabc, где L - апофема
S=1/2*3*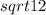 *4+3*
*4+3*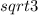 =15
=15