Номер 1
Можно даже не вычислять,чему равны углы 1;2;3;
Два угла 30 градусов называются соответственными,если при пересечении двух прямых секущей соответственные углы равны,то прямые параллельны
<1=<30=30 градусов,как накрест лежащие,вообще-то-смотрятс каким из двух углом сравнивать
<1+<2=180 градусов,как односторонние
<2=180-30=150 градусов
Если при пересечении двух прямых секущей односторонние углы в сумме равны 180 градусов,то прямые параллельны
<3=<2=150 градусов,как вертикальные
Номер 2
<20=<2=<20 градусов,как вертикальные
Если угол 3 в 8 раз больше угла 2,то
<3=20•8=160 градусов
<3=20+160=180 градусов
Если при пересечении двух прямых секущей односторонние углы в сумме равны 180 градусов,то прямые параллельны
<4=<3=160 градусов,как накрест лежащие
<5=<2=20 градусов
Объяснение:
Внешний угол при вершине треугольника равен сумме внутренних углов треугольника, не смежных с ним. Рассмотрим треугольник АВС. Угол СВН - внешний угол при вершине, противоположной основанию. BM- биссектриса этого угла. Она делит угол на два равных угла 1 и 2. Так как внешний угол при В равен сумме внутренних углов А и С, а треугольник АВС равнобедренный и углы при его основании равны между собой, все выделенные углы также равны между собой. Углы под номером 1-равные соответственные при прямых АС и Bм и секущей АВ Углы под номером 2 -равные накрестлежащие при прямых АС и ВМ и секущей ВС Если при пересечении двух прямых третьей внутренние накрестлежащие углы равны, то прямые параллельны.
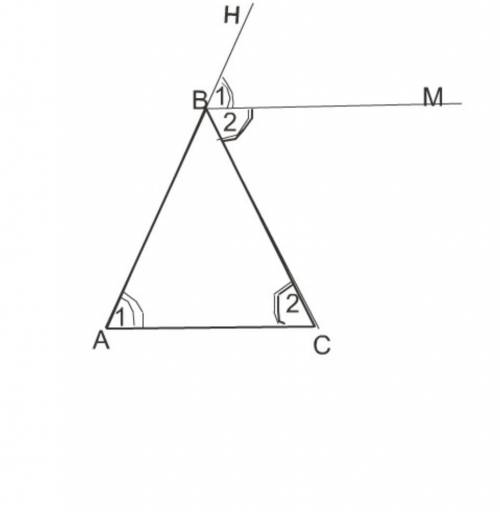
(Рисунок во вложении)
Есл, что пункты Н, К, Р, М я добавил для обозначения некоторых углов
Угол САВ = углу ДВК (соответственные), а угол КВД = углу ВДС (накрест лежащие), значит угол САВ = углу ВДС
Угол АВД = углу ВДМ ( накрест лежащие), а угол ВДМ = углу АСД ( соответственные углы), значит угол АВД = углу АСД
Раз угол САВ = углу ВДС, а угол АВД = углу АСД, то АВСД - параллелаграмм, и значит АС = ВД (противоположные стороны параллелограмма равны)