
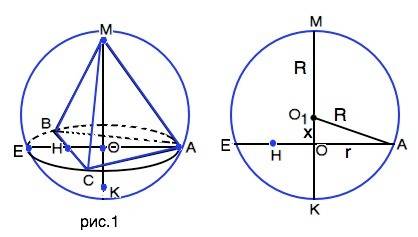
Обозначим пирамиду МАВС, центр шара О1, его диаметр МК.
Высота пирамиды МО=10 см. Сторона основания АВ=АС=ВС=9 см.
Основание пирамиды лежит в плоскости описанной вокруг него окружности с центром О. (см.рис.№1)
Радиус описанной окружности правильного треугольника равен а/√3: ОА=9/√3=3√3,
Рассмотрим схематический рисунок.
Пусть ОО1 -расстояние от центра шара до центра основания пирамиды равно х. Тогда R=10-х.
Из прямоугольного ∆ АОО1
R²= АО1*=OO1²+AO²=x²+27
R²=(10-x)²=100-20x+x²; R²=R² ⇒
x*²+27=100-20x+x² откуда
20х=73; х=3,65; ⇒R=10-3,65=6,35 см
По формуле объема шара V=4πR²/3= ≈1072,53 см³
Первый вопрос: 1). Докажем, что плоскость ABCD параллельна плоскости A1B1C1D1. Для этого построим пары диагоналей AC, BD, а также A1C1, B1D1.
2). Теперь рассмотрим треугольник OBD. Прямая B1D1 параллельна прямой BD, как средняя линия треугольника OBD, т.к. B1D1 соединяет середины его сторон B1 и D1 (эти точки середины по условию).
3). Теперь рассмотрим треугольник OAC. Прямая A1C1 параллельна прямой AC, как средняя линия треугольника OAC, т.к. A1C1 соединяет середины его сторон A1 и C1 (эти точки середины по условию).
4). Тогда получаем, что две пересекающиеся прямые AC и BD плоскости ABCD параллельны двум пересекающимся прямым A1C1 и B1D1 плоскости A1B1C1D1, а из этого, по теореме о параллельности двух плоскостей, следует, что плоскости ABCD и A1B1C1D1 параллельны, что и требовалось доказать.
Второй вопрос: 1). Рассмотрим треугольник OBA. B1A1 - средняя линия треугольника OBA, т.к. соединяет середины сторон OB и OA (B1 и D1 середины по условию). Тогда B1A1=1/2 AB=10/2=5.
2). Аналогично B1C1 - средняя линия треугольника BC, C1D1 - средняя линия треугольника CD, A1D1 - средняя линия треугольника AD.
3). Тогда, B1C1=5, C1D1=5, A1D1=5.
4). Периметр A1B1C1D1=B1C1+C1D1+A1D1+B1A1=5+5+5+5=20