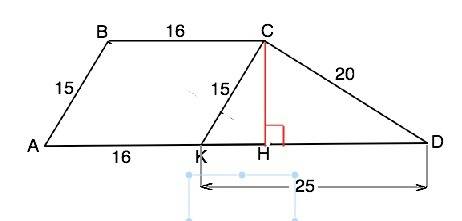
Обозначим вершины трапеции АВСD. Стороны: АВ=15, ВС=16, СD=20, AD=41. Из вершины С проведем СК параллельно АВ. Тогда АВСК - параллелограмм, и СК=15 см, АК=ВС=16 см, КD=AD-AK=25 см. Отношение сторон ∆ СКD=15:20:25, т.е. 3:4:5. ⇒ ∆ КСD - так называемый египетский, он прямоугольный. Площадь ∆ КСD=KC•CD:2=150 см². Тогда его высота СН=2S:KD=300:25=12 см (она же высота трапеции АВСD). Площадь трапеции равна половине произведения высоты на сумму оснований. S(ABCD)=CH•(BC+AD):2=12•57:2=342 см²
Подобных задач с полным и правильным ответом на сайте немало. При желании можно найти другие варианты решения.
Дано:
S(ABCD) = 8 см²
DF = 5 см
----------------------------
BF - ?
Решение.
ΔBFD - прямоугольный треугольник, ⇒
⇒ BF = √(DF² - DB²)
DB = AB√2 (диагональ квадрата это его сторона на √2)
S(ABCD) = AB² ⇒
⇒ AB = √S(ABCD)
AB = √8 = 2√2
DB = 2√2 * √2 = 4
BF = √(5² - 4²) = √(9) = 3 см
ответ: BF = 3 см