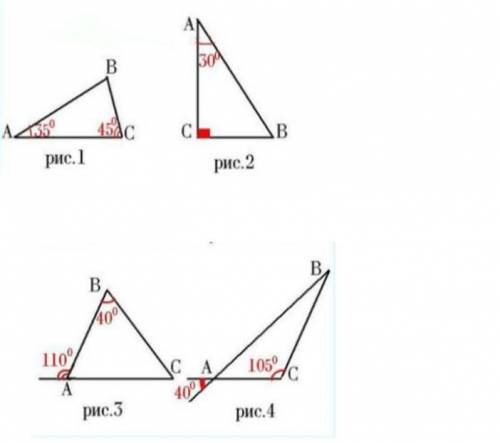
1)такого не може існувати.
2)кут В=60° , а кут С=90°
3)кут А=70°, а С=70°
4)кут А=40°, а кут В=35°
Объяснение:
1)180°-(135°+45°)=0
2)180°-(90°+30°)=60°
3)180°-110°=70°
180°-(40°+70°)=70°
4)кут А теж 40° тоді 180°-(105+40°)=35°
а) ∆АВС - рівнобедрений (АВ = ВС).
Нехай зовнішній кут 130° - це кут при вершині.
∟DBC = 130°, тоді ∟DBC = ∟A + ∟C.
∟A + ∟C = 130°. ∟A = ∟C = 130° : 2 = 65° (кути при ocнові).
∟B = 180° - ∟DBC. ∟B = 180° - 130°; ∟B = 50°.
Biдповідь: 65", 65°, 50°.
б) ∆АВС - рівнобедрений (АВ = ВС).
Нехай зовнішній кут 130° - це кут при основі ∟BCD = 130°,
тоді ∟BCD + ∟BCA = 180°.
∟BCA = 180° - 130° = 50°; ∟BCA = ∟BAC = 50°
(кути при ocновi рівнобедреного трикутника).
∟BAC + ∟BCA + ∟B = 180°.
∟B = 180° - (50° + 50°) = 180° - 100° = 80°.
Biдповідь: 50°, 50°, 80°.
ответил 08 Янв, 17 от discere
Пусть N- середина АС. Тогда BN перпендикулярно плоскости ADC, поскольку BN перпендикулярно АС (медиана равнобедренного треугольника) и AD (BN лежит в плоскости ABC).
BN = AC/2 = 2√2; это - расстояние от точки В до плоскости ADC.
Поскольку точка М лежит на наклонной прямой DB посредине между D и B, расстояние от M до плоскости ADC равно h = BN/2 = √2;
это можно считать высотой пирамиды ALCM , за основание принята грань ALC, осталось сосчитать её площадь.
AL - высота в прямоугольном треугольнике ACD, где AD = 4; AC = 4√2; откуда DC = 4√3;
AL = AD*AC/DC = 4√(2/3);
При этом из подобия ADC и ALC
LC/AL = AC/AD = √2; LC = 8/√3;
Площадь ALC равна S = LC*AL/2 = 16√2/3;
Объем ALCM равен V = S*h/3 = 32/9;
обязательно проверьте всю арифметику
рис. 1 тут не могут быть такие углы ,потому что
180° - (135°+45°)= 0
рис 2. 90°-30°= 60° углы А30° С90° В60°
рис. 3 В=40°
А = 180°-110°=70°
С= 110°-40°= 70°
рис. 4 С= 105°
А= 40°
В= 180°-(105°+40°)= 35°