по теорме пифагора
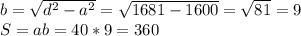
1) 
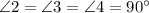; 2) Величина острого (наименьшего) угла.
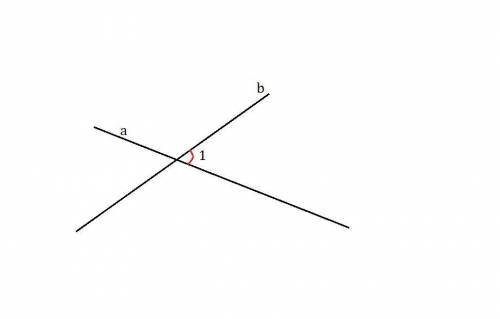
1) Начертим две пересекающие прямые. Обозначим их буквами 
и 
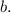
При их пересечении, образовался угол в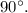 
Пусть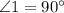 
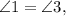как вертикальные.
.
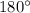и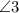 
- смежные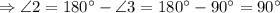 
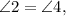как вертикальные.
2) Угол между двумя пересекающимися прямыми - это величина наименьшего угла между двумя пересекающимися прямыми.
Обозначим две пересекающиеся прямые буквами и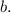
При пересечении произвольных прямых, образуются 4 угла: 2 равных тупых угла и 2 равных острых угла (они равны, как вертикальные).
В данном случае наименьший угол - это величина острого угла, так как величина острого угла меньше тупого.
=============================================================
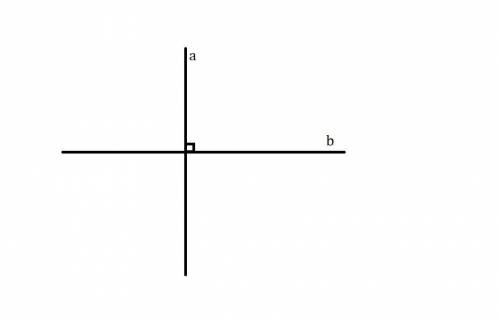
Но если прямые перпендикулярные (прямые, при пересечении которых образуются 4 прямых угла), то наименьший угол - это величина прямого. Но в данной задаче этого не уточняется, поэтому верный ответ - величина острого угла.
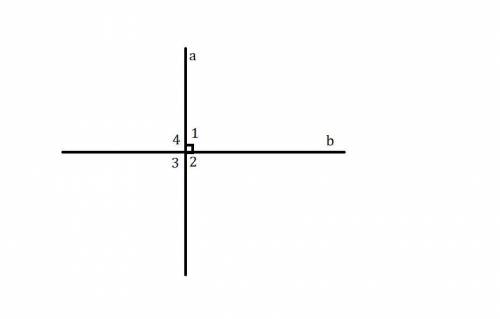
по т Пифагора найдем вторую сторону=9 (9*9+40*40=41*41)
S=40*9=360