9
Объяснение:
В плоскости, на равном расстоянии от вершин треугольника, находится центр окружности, описанной около этого треугольника, при этом прямой угол опирается на дугу 180° (вписанный угол равен половине дуги, на которую опирается), а это значит, что гипотенуза прямоугольного треугольника является диаметром окружности, описанной около этого треугольника, а середина гипотенузы является центром этой окружности.
Следовательно, если из середины гипотенузы восстановить перпендикуляр над плоскостью треугольника, то точка А будет находиться на этом перпендикуляре на расстоянии 4 от плоскости.
1) Длина гипотенузы треугольника:
с = √(8²+14²) = √(64+196) = √260
4) Расстояние d от точки А до вершин треугольника, согласно теореме Пифагора:
d² = (√260/2)² + 4² = 260/4 + 16 = 65 + 16 = 81
d = √81 = 9
ответ: 9
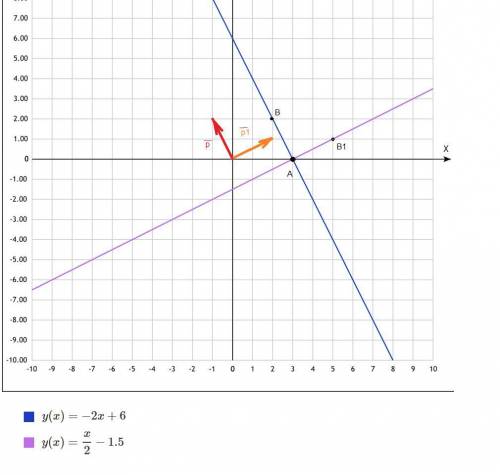
а) Найду точку В , в которую с вектора Р перейдет А и напишу уравнение прямой через 2 точки
B(3-1;0+2)=(2;2)
y=kx+b
подставив обе точки получу систему
0=3k+b
2=2k+b
вычитаю из первого второе
-2=k
подставлю в первое
0=3*(-2)+b
b=6
y=-2х+6-уравнение прямой
б)если р-нормаль, найду р1-перпендикулярный ему вектор, который будет направляющим вектором прямой и все решу как в случае а
p*p1=0
(-1;2)*(x;y)=0
-x+2y=0
x=2y
p1(2;1) например....
B1(3+2;0+1)=(5;1)
уравнение через А и В1 выведу
система
0=3k+b
1=5k+b
решаю ее
-1=-2k
k=0.5
в первое
0=1.5+b
b=-1.5
y=x/2-1.5-уравнение прямой