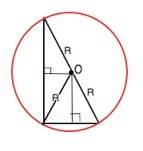
Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы.
По т.Пифагора с²=a²+b², где с - гипотенуза, a и b – катеты.
с=√(9²+12²)=15
R=15:2=7,5 см
Подробно.
Центр описанной окружности треугольника лежит на пересечении срединных перпендикуляров к его сторонам.
Срединные перпендикуляры прямоугольного треугольника пересекаются на середине гипотенузы, следовательно центр описанной окружности - середина гипотенузы, и радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. R=7,5 см.
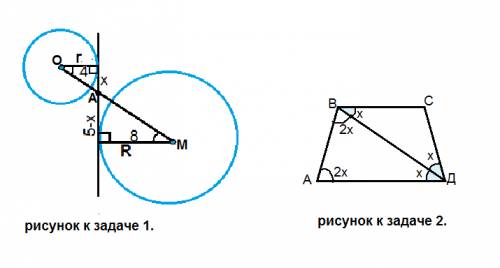
Пусть AB=h
Тогда BC^2=10^2-h^2
BD^2=17^2-h^2
BC и BD и есть проекции AD и AC.
BC^2 : BD^2 = 4 : 25
25*(10^2-h^2)=4*(17^2-h^2)
50^2-25h^2=34^2-4h^2
50^2-34^2=25h^2-4h^2
16*84=21h^2
16*4=h^2
h=8
ответ AB=8