Объяснение:
у=4х-7
Точка А имеет координаты (8,2;25,8), где абсцисса х=8,2.
ордината у=25,8.
Подставим значение х и у в график, и проверим уравнивается правая и левая часть.
25,8=4*8,2-7
25,8=32,8-7
25,8=25,8
Точка А(8,2;25,8) принадлежит графику у=4х-7
2)
т.В(-71;-290)
х=-71
у=-290
у=4х-7, подставляем значение х и у.
-290=4(-71)-7
-290=-284-7
-290≠291
Правая и левая часть не уравнялись, значит т.В(-71;-290) не принадлежит этому графику.
3) т.С(35;-133)
х=35
у=-133
у=4х-7, подставляем значение х и у.
-133=4*35-7
-133=140-7
-133≠133
т.С не принадлежит графику у=4х-7.
4) т.D(-46;-191)
x=-46
у=-191
у=4х-7
-191=4(-46)-7
-191=-184-7
-191=-191
т.D(-46;-191) принадлежит этому графику.
Бог в
Вступление:
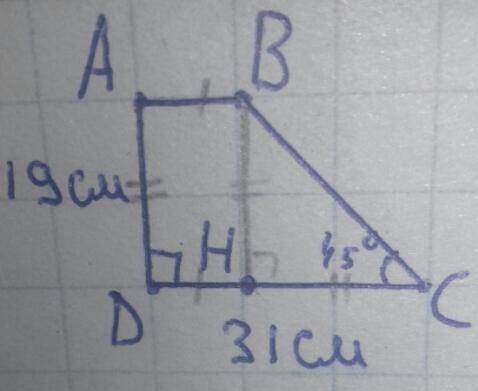
Пусть в прямоугольной трапеции ABCD, AB и CD основания, а ∠D прямой. Тогда AD меньшая боковая сторона (как расстояние между параллельными отрезками AB и CD), то есть AD=19см. По построению DC большое основание, поэтому по условию DC=31см. Острые углы при большом основании, ∠C=45° т.к. ∠D=90°.
H∈DC, BH⊥DC ⇒ BH=AD=19см.
В прямоугольном ΔBHC:
∠C=45°, ∠H=90° ⇒ ∠B=45°⇒ HC=BH=19см.
DH=DC-HC=31-19=12см.
В четырёхугольнике ABHD:
∠D=90°, ∠H=90° и ∠A=90°, ∠B=90° т.к. AB║DH, ведь H∈DC и AB║DC.
Получается ABHD - прямоугольник, поэтому AB=HD, HD=12см ⇒ AB=12см.
AB мень. осн. т.к. CD - большее.
Меньшее основание равно 12см.
1. рассм. BOC равнобедренный так как OB=OC=r
след-но углы при основании равны - угол OBC = OCB = 34
тогда угол BOC = 180-34-34 = 112
угол BOC = углу AOD - вертикальные
след-но угол AOD = 112
2.
тр-к ABC прямоугольный. Радиус описанной окружности около прям тр-ка раdен половине гипотенузы ⇒ AB = 2*2.5 = 5
AC=√AB²-BC²=√25-16=√9=3