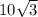
Объяснение:
Радиус описанного круга равняется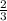
высоты треугольника;Высота треугольника равняется стороне на синус угла то есть 
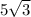на синус 60° (7,5 см)R=5смПоловина стороны шестиугольника равна радиусу на тангенс 60° (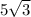)Полная сторона шестиугольника равна двум половинкам, то есть 
.
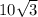Внешний угол треугольника - это угол, смежный с внутренним углом треугольника.
Т.к. треугольник прямоугольный, то один из углов равен 90°, тогда сумма острых его углов тоже равна 90°. Угол, смежный с прямым углом, тоже прямой.
По условию один из внешних углов равен 120°, тогда смежный с ним внутренний равен 180° - 120° = 60°. Тогда втрой острый угол прямоугольного треугольника равен 90° - 60° = 30°.
Таким образом, прямоугольный треугольник имеет углы 90°, 60° и 30°.
Наибольшая сторона лежит против наибольшего угла, т.е. против прямого угла, и эта сторона - гипотенуза.
Наименьшая сторона лежит против наименьшего угла, т.е. - это катет, лежащий против угла в 30°.
Есть такое свойство катета прямоугольного треугольника, лежащего против угла в 30°: катет, лежащий против угла в 30°, равен половине гипотенузы.
По условию сумма наибольшей и наименьшей сторон прямоугольного треугольника равна 18 см, т.е. это сумма катета, лежащего против угла в 30° и гипотенузы.
Пусть катет равен х см, тогда гипотенуза равна (2х) см. Составим и решим уравнение:
х + 2х = 18,
3х = 18,
х = 18 : 3,
х = 6.
Значит, катет равен 6 см, тогда гипотенуза равна 2 · 6 = 12 (см)
ответ: 12 см и 6 см.
Объяснение:
1) Радіус кола, описаного навколо правильного трикутника:
R = a3√3/3 = 5√3*√3/2 = 5см.
Це ж коло вписана в правильний шестикутник. Тоді сторона правильного шестикутника:
a6 = 2r * tg(180°/6) = 2r * tg(30°) = 2r * √3/3
r = R = 5см.
a6 = 2*5*√3/3 = 10√3/3.