Не знаю, насколько правильно, но все же
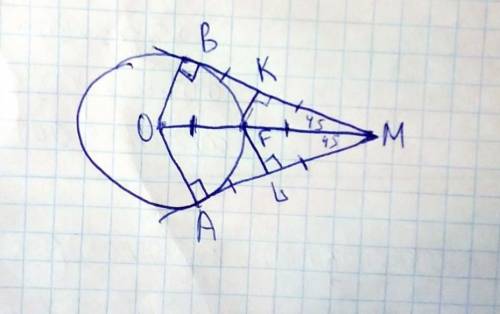
Проведём радиусы OB, OA. Они образуют прямые углы с касательной(по свойству). Значит ОВ перпенликулярна ВК, а ОА перпенликулярно АМ.
Также я указала точку F.
Теперь проведём прямые FK и FL, которые будут параллельны прямым OB и OA соответсвенно. Значит, они будут также перпендикулярны к BM и AМ соответственно.
ВО и KF параллельны и OF=FM. Значит по теореме Фаллеса ВК=КМ
Аналогично ОА//FL и OF=FM. Также по т. Фаллеса AL=LM
Теперь рассмотрим треугольники KFM и LFM. Они будут прямоугольными и равнобедренными(углы K, L-прямые, КМ=МF=ML). Значит, углы при катетах будут 45 градусов, а именно углы KMF, KFM, LFM, LMF
Угол АMB состоит из углов KMF и FML. А они по 45. Значит, угол АМВ=45*2=90
ответ: 70°
Объяснение: Соединим точки А и В и получился ∆АОВ с углом АОВ =130°
Этот треугольник равнобедренный, поскольку АО=ВО=радиусу, а значит угол ОАВ= углу АВО. Зная что сумма углов треугольника составляет 180°найдём сумму равных углов: 180-110=70°. Так как они равны, то угол ОАВ=углу АВО=70÷2=35°. Рассмотрим ∆АВС. Он также является равнобедренным, поскольку прямые соединяются в одной точке и АС=ВС. Радиус, проведённый к точке касания образует с ней прямой угол 90°, поэтому угол ВАС=углу СВА=90-35=55°. Теперь найдём угол С:
180-2×55=180-110=70°; итак: угол С=70°
Обозначим ВК высоту, опущенную из вершины В на основание АД, а высоту, опущенную из вершины С на основание АД - СМ,
По условию АК = 3см, а ДК= 7см.
ДК= ДМ + КМ
МД = АК = 3см, т.к трапеция равнобедренная и тр-к АВК = тр-ку ДСМ. Тогда
КМ = ДК - ДМ = 7 - 3 = 4(см)
ВС = КМ = 4см, т.к ВКСМ - прямоугольник.
Площадь трапеции равна произведению полусуммы оснований и высоты.
Основания: АД = АК + ДК = 3 + 7 = 10(см)
ВС = 4см
Высота задана ВК = 4см
Площадь трапеции:
S = 0.5·(10 + 4)·4 = 28(cм²)