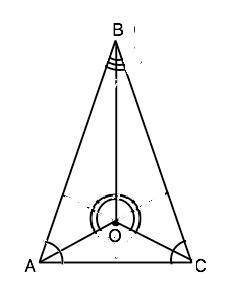
О - точка пересечения биссектрис треугольника АВС.
∠AOB = ∠COB. Найти наименьший угол треугольника ABC, если ∠ABC в три раза меньше ∠AOC
ответ: 36°
Объяснение:
ВО- биссектриса угла В, ∠AOB =∠COB (дано)⇒
∆ АОВ=∆ СОВ по двум углам при общей стороне ВО ( 2-й признак). ⇒
∠ВОА=∠ВОС.
Т.к. АО и СО - биссектрисы, то и ∠ВАС=∠ВСА. как состоящие из равных половинок. ⇒ ∆ АВС равнобедренный.
Примем ∠ОАС и ∠ОСА равными α. Тогда ∠АОС=180°-2α.
∠АВС=180°-4 α.
Составим уравнение согласно условию:
∠ АОС=3∠ АВС⇒
180°-2α=3(180°-4α). Произведя необходимые вычисления, получим 10α=360°⇒ α=36°
Угол АВС=180°-4•36°=36°.
Углы А и С вдвое больше α, они равны по 72°.
Следовательно, наименьший угол ∆ АВС - угол АВС=36°
6,6 см
Объяснение:
Оскільки трапеція прямокутна, то два кути в неї будуть по 90 градусів. проведемо висоту з тупого кута. Ця висота більшу основу на відрізки, один з яких буде дорінювати меншій основі, як сторона прямокутника. Знаючи довжину одного з відрізків знайдемо другий відрізок
9,5-2,9=6,6 см. Цей відрізок буде стороною рівнобедреного прямокутного трикутника, оскільки висота проведена до відрізка під кутом 90, а другий її кут 45 градусів. Тому за властивістю рівнобедреного трикутника довжина відрізка дорівнює довжині висоти і дорівнює 6,6,см, а оскільки менша бокова сторона прямокутної трапеції є висотою, то в трапеції висоти рівні і дорівнюють 6,6 см
Треугольник АВС - равнобедренный, следовательно АВ=ВС=13 см, в равнобедренном треугольнике медиана является высотой, а высота в равнобедренном треугольнике точкой пересечения делит основание АС пополам (следовательно АН=НС). АН - высота. АН=5 см.
Высота треугольника перпендикулярна основанию, след-но треугольник ВНС - прямоугольный, по теореме Пифагора получим: НС=sqrt(13^2-5^2)=sqrt(144)=12 см.
Т.к. АН=НС=12 см, следовательно АС=12+12=24 см.
S_авс=1/2*ВН*АС=1/2*24*5=60 см^2.
Р_авс=АВ+ВС+АС=13+13+24=50 см.
ответ: S_авс=60 см^2; Р_авс=АВ+ВС+АС=50 см.