здесь типо как обьяснить тебе,

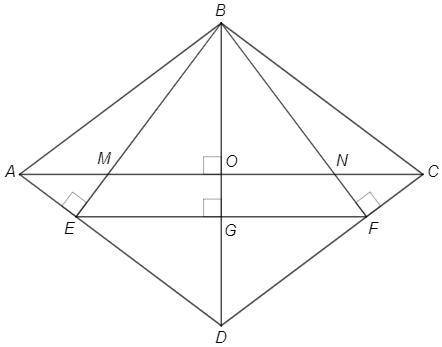
Ромб - стороны равны, противоположные углы равны, диагонали перпендикулярны.
Треугольники ABE и CBF равны по гипотенузе и острому углу, AE=CF.
Точки E и F делят стороны ромба в равном отношении => AC||EF => EF⊥BD
S(ABO) =1/4 S(ABCD) =1/4 *1/2 *160*120 =2400
AB =√(AO^2 +BO^2) =100
∠ABD=∠ADB => △ABO~△BDE
BE/AO =BD/AB => BE =80*120/100 =96
△BEG~△BMO~△BDE => △BEG~△BMO~△ABO
S(BEG)/S(ABO) =(BE/AB)^2 =(96/100)^2 =0,96^2
S(BMO)/S(ABO) =(BO/AO)^2 =(60/80)^2 =0,75^2
S(MOGE) =S(BEG)-S(BMO) =2400 (0,96^2 -0,75^2) =861,84
S(MNFE) =2 S(MOGE) =1723,68
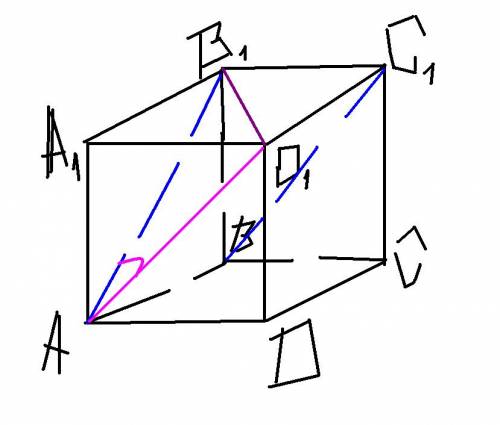
а) BC1 || AD1, поэтому угол между прямыми AB1 и BC1 равен углу между AB1 и AD1.
ребро куба равно а, поэтому (так как грани куба - квадраты), то AB1=AD1=B1D1, а значит треугольник AB1D1 - правильный(равносторонний),
углы равностороннего треугольника равны 60 градусов,
значит искомый угол между прямыми AB1 и BC1 равен 60 градусов
б) так как В1С1 - перпендикуляр с точки С1 на грань АА1В1В, то угол между прямой AC1 и гранью AA1B1B равен углу В1АС1
(треугольник АВ1С1 - прямоугольным с прямым углом АВ1С1)
по свойству диагонали квадрата 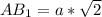
по свойству диагонали куба 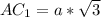
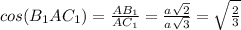
угол В1АС1 равен arccos корень(2/3)т.е.
угол между прямой AC1 и гранью AA1B1B равен arccos корень(2/3) градусов
1
АВ/А1В1=10/15=2/3
ВС/В1С1=5/7,5=2/3
АС/А1С1=7/9,5=14/19
2/3≠14/19
Не подобны
2
<C=180-<A-<B
<C=180-37-48=95
<B=<B1 и <C=<C1
Подобны по 2 равным углам (1 признак)
3
АС=√(АВ²-ВС²)=√(100-64)=6
АВ/А1В1=10/5=2
АС/А1С1=6/3=2
Подобны по 2 пропорциональным сторонам и углу между ними (2признак)
Объяснение: