Задача 1 (рисунок 1).
1) МВ и КВ, МА и ТА, КС и ТС - отрезки касательных, проведённых из одной точки. Они равны по свойству касательных. Следовательно, треугольник АВС разбивается на три пары равных (попарно) отрезков.
PΔАВС=2*2+4*2+6*2=24см.
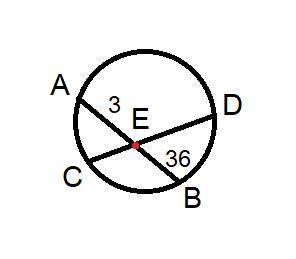
Задача 2 (рисунок 2).
3:4=3х+4х
По теореме о пересекающихся хордах:
36*3=3х*4х
108=12х²
х=3.
CD=3*7=21см.
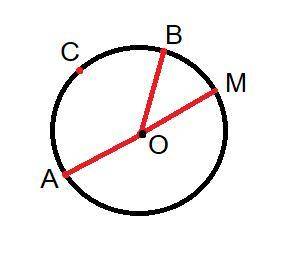
Задача 3 (рисунок 3).
Сначала ищем градусную меру дуг АМВ и АСВ.
Если 2 дуги, на которые делит окружность любая хорда, вместе равны 360°, то:
(360-80):2=140° - дуга АСВ.
Тогда дуга АМВ = 140+80=220°. (в сумме 360).
Дальше пользуемся свойствами вписанных и центральных углов:
1) ∠АСВ=150°, ∠АОВ=210° (центральные ∠).
2) ∠АМВ=половине АОВ=75°, ∠АВМ=половине АОМ=90°,
3)∠АСВ=половине АМВ=105° (вписанные углы).
ответ: 210° - ∠АМВ, 90° - ∠АВМ, 105° - ∠АСВ.
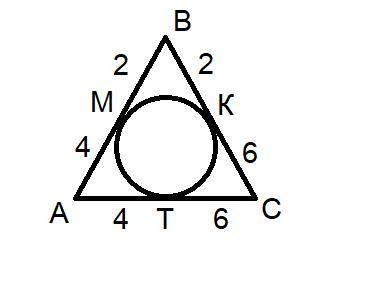
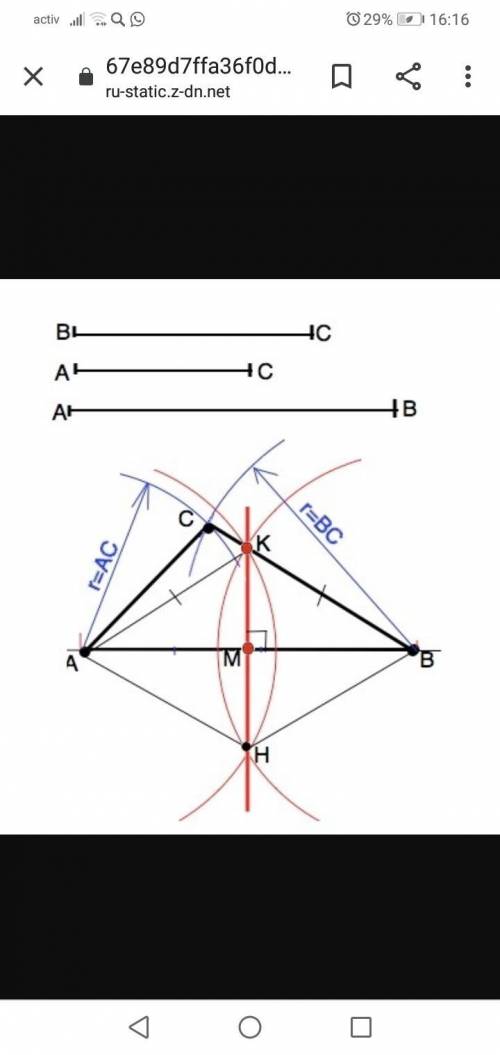
ответ:. На произвольной прямой отложить отрезок, равный стороне АВ. Обозначить вершины треугольника: точки А и В.
2) Из точки А как из центра раствором циркуля радиусом, равным длине стороны АС, начертить дугу.
3) Из т.В как из центра раствором циркуля радиусом, равным длине стороны ВС, начертить дугу до пересечения с первой дугой.
Точка пересечения дуг - вершина С искомого треугольника.
б) Построение срединного перпендикулярна стандартное.
Из т.А и т.В как из центров провести полуокружности произвольного, но равного радиуса, но больше половины АВ так, чтобы они пересеклись по обе стороны от АВ (т.К и т. Н).
Точки пересечения К и Н этих полуокружностей соединить.
Соединить А и Н, В и Н. Четырехугольник АКВН - ромб ( стороны равны взятому радиусу). Диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам. =>
АМ=МВ и КМ перпендикулярно АВ.
КМ - срединный перпендикуляр к стороне АМ.
Точно так же делят отрезок пополам.
Объяснение: делал на скорую руку
cosA= ac/ab 1/2=6/AB AB=12