
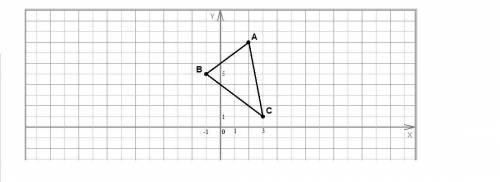
cos∠B = 0
cos∠A = 0,6
cos∠C = 0,8
Объяснение:
Найдем длины сторон треугольника по формуле расстояния между точками:
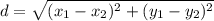
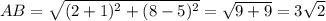
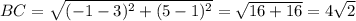

Проверим по теореме, обратной теореме Пифагора, не является ли этот треугольник прямоугольным:
AC² = AB² + BC²
(5√2)² = (3√2)² + (4√2)²
50 = 18 + 32
50 = 50 - равенство верно, значит треугольник прямоугольный с гипотенузой АС.
Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.
Косинус прямого угла равен нулю.
cos∠B = 0
cos∠A = AB / AC = 3√2 / 5√2 = 3/5 = 0,6
cos∠C = BC / AC = 4√2 / 5√2 = 4/5 = 0,8
Найдите сумму координат вершины С параллелограмма ABCD, если известно, что А(-5; 2; 8), AB(-3; 4; 1) и BD(-2; 4; 1).
Объяснение:
Из условия А(-5; 2; 8), AB(-3; 4; 1) найдем координаты точки В:
х(АВ)= х(В)-х(А) у(АВ)= у(В)-у(А) z(АВ)= z(В)-z(А)
х(В)= х(АВ)+х(А) у(В)= у(АВ)+у(А) z(В)= у(АВ)+у(А)
х(В)= -3+(-5)=-8 у(В)= 4+2=6 z(В)= 1+8=9 .
В(-8; 6; 9).
Из условия В(-8; 6; 9) , BD(-2; 4; 1). найдем координаты точки D:
вычисления аналогичные :
х(D)= -2+(-8)=-10 у(D)= 4+6=10 z(D)= 1+9=10 .
D(-10; 10; 10).
Пусть координаты точки С(х;у;z), тогда координаты DC( х+10;у-10;z-10).
АВСD-параллелограмма, значит вектора равны АВ=DC⇒ координаты равны :х+10=-3 , у-10=4 , z-10=1
х= -13 , у=14, z=11 . Сумма этих чисел :-13+14+11 =12.