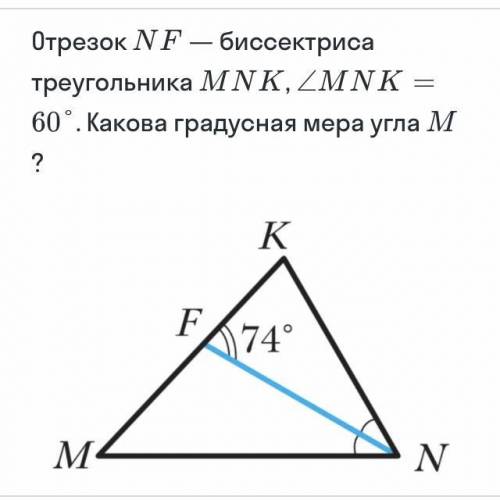
∡ Δ FNK. ∠FNK = 60° : 2 = 30° (как биссектриса), а ∠NFK = 74° (по условию), тогда ∠FKN = 180° - (74° + 30°) = 76°.
∠M = 180° - (∠K + ∠N) = 180° - (76° + 60°) = 180° - 136° = 44°
ответ: 44°.
Рассмотрим треугольник АВС. Он равнобедренный по условию, так как боковые стороны у него равны. Значит, углы при основании тоже равны - по свойству равнобедренного треугольника.
Так как по условию треугольник АВС ещё и прямоугольный, то сумма его острых углов даёт 90° - по свойству прямоугольного треугольника.
Найдем углы при основании:
BAC = ACB = 90° : 2 = 45°.
Далее рассмотрим углы АСВ и ЕСD - они вертикальные, значит АСВ = ЕСD = 45°.
Так как треугольник СЕD по условию тоже равнобедренный (боковые стороны у него равны по условию), то углы при основании равны. Отсюда находим угол СЕD, он же угол х:
(180° - угол ЕСD) : 2
(180° - 45°) : 2 = 67,5° - угол х.
Рассмотрим треугольник АВС. Он равнобедренный по условию, так как боковые стороны у него равны. Значит, углы при основании тоже равны - по свойству равнобедренного треугольника.
Так как по условию треугольник АВС ещё и прямоугольный, то сумма его острых углов даёт 90° - по свойству прямоугольного треугольника.
Найдем углы при основании:
BAC = ACB = 90° : 2 = 45°.
Далее рассмотрим углы АСВ и ЕСD - они вертикальные, значит АСВ = ЕСD = 45°.
Так как треугольник СЕD по условию тоже равнобедренный (боковые стороны у него равны по условию), то углы при основании равны. Отсюда находим угол СЕD, он же угол х:
(180° - угол ЕСD) : 2
(180° - 45°) : 2 = 67,5° - угол х.
ответ:44⁰
Объяснение: