Все три точки будут находиться на одной прямой, и расстояние от Х₁ до Х₃ равно сумме длин отрезков Х₁Х₂ и Х₂Х, а именно 10+12=22.
Объяснение тому, что все три точки находятся на одной прямой, нужно искать в построения сечений многогранников плоскостью методом следов.
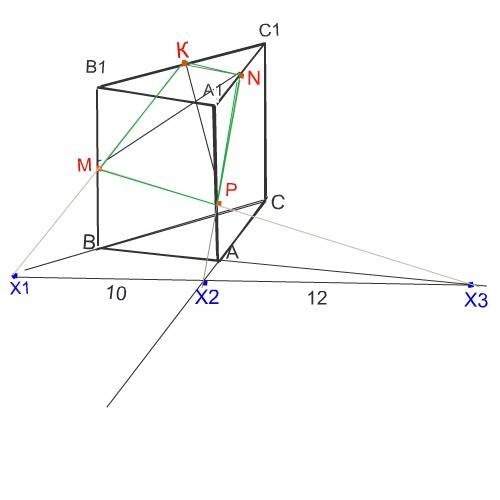
Подтверждение тому то. что прямые MN и KР пересекаются и принадлежат одной плоскости.
Х₁, Х₂, Х₃ тоже принадлежат той же плоскости. Прямая Х₁Х₃ - линия пересечения этой плоскости с плоскостью, которой принадлежит основание призмы. Продолжить принадлежащую той же плоскости КN на рисунке нет просто места.
Но соглашусь только с первыми четырьмя с половиной строками. Далее: отрезки 9см и12см не есть отрезками диагоналей (центр вписанной окружности равноудален от оснований, а точка пересечения - ближе к меньшему основанию, посмотрите подобие двух треугольников при основаниях).
С пятой строки так:
Боковая сторона CD=√(144+81)=√225=15=AB. Если в четырехугольник вписана окружность, то суммы длин его противолежащих сторон равны. Для данной трапеции сумма оснований равна сумме боковых сторон, BC+AD=AB+CD=30.
Теперь найдем высоту. h=2r, тк радиусы перпендикулярны основаниям. В трOCD OK=r -перпендикуляр к CD. Из подобия тр OKD и тр COD запишем: r/12=9/15; r=36/5. h=2r=72/5. S=(15*72)/5=216.
Нарисуйте рисунок.