Объяснение: ∠АВD=46°
Объяснение:
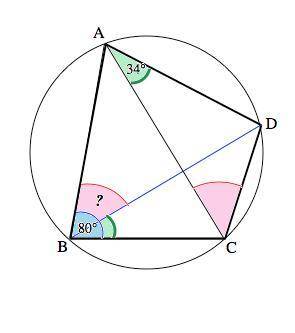
Четырехугольник ABCD вписан в окружность.
Дается два варианта решения.
а) Сумма противоположных углов вписанного в окружность четырехугольника – 180°. =>
∠ADC=180°-80°=100°. Тогда из суммы углов треугольника в ∆ АDС
∠ ACD=180°-(<ADC+DAC)=46°
Вписанные углы, которые опираются на равные дуги, равны.
∠АВD и ∠АCD опираются на одну дугу DC =>
——————
б) Углы CВD и САD опираются на одну дугу DC.
Вписанные углы, которые опираются на равные дуги, равны. => ∠CВD=∠CAD=34°
∠АВD=∠АВС- ∠СВD=80°-34°=46°
Объяснение:
6(2)
Дано: ромб
диагонали ромба d₁ = 16 дм; d₂ = 30 дм
Найти: сторону ромба а - ?
Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре, а все стороны ромба равны. значит можем найти сторону
ромба
4а² = d₁² + d₂²
4а² = 16²+30²=256+900=1156
а² = 289; а = 17 (дм)
7)
Дано: стороны прямоугольника а = 16 см, с = 91 см
Найти: диагональ прямоугольника d - ?
диагональ прямоугольника делит прямоугольник на два прямоугольных треугольника. берем один из них и видим, что диагональ d - это гипотенуза прямоугольного треугольника со сторонами 60 и 91. тогда по теореме Пифагора
d² = а² + с²
d² = 16² + 91² = 3600 + 8281 = 11881
d = 109 (см)
9)
окружность описана вокруг квадрата.
диаметр окружности d = 1.4 (м); радиус r = 0.7(м)
сторона квадрата а = 1 (м)
сторона квадрата и диаметр описанной окружности связаны формулой
r= a/√2
проверяем 0,7 ≈ 1/√2
ответ - можно