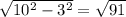. Значит, вся диагональ -- 
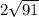, а сторона квадрата, которая в 
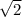раз меньше, чем диагональ, равна 
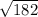. Таким образом, боковая грань представляет собой треугольник со сторонами 10, 10, 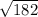. Площадь этого треугольника можно найти, например, опустив высоту из вершины, (эта высота будет и медианой). Получается, высота равна 
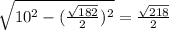, откуда площадь одного треугольника равна 
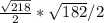, а площадь боковой поверхности равна площади четырёх таких треугольников, т. е. 
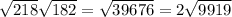Может, обсчитался где-то.
тогда
ВМ = МС, В1М1 = М1С1 (АМ и А1М1 - медианы),
а раз ВС = В1С1, то все педидущие четыре отрезка равны:
ВМ = МС = В1М1 = М1С1
далее уголВ = углуВ1(соответствующие углы равных треугольников)
АВ = А1В1 (соответствующие стороны равных треугольников)
на основании выше изложенного делаем вывод, что тр.АВМ = тр.А1В1М1(по двум сторонам и углу между ними)
а уже на основании равенства треугольников АВМ и А1В1М1 делаем вывод о равенстве наших медиан АМ и А1М1, что и требовалось доказать