Можно было бы, конечно, находить высоту к основанию и т. д., но, если подумать, то можно вспомнить, что в равнобедренном прямоугольном треугольнике (да-да наш треугольник является именно таким, посольку углы при основании равны 45), боковые стороны являются взаимными высотами. таким образом:
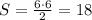 см²
см²
Короче его площадь равна как бы половине квадрата со стороной 6 см, разрезанного по диагонали, из рисунка это совершенно очевидно. Как-то так...
Ну и, как "Лучшее решение" отметить не забудь, разумеется, ОК?!.. ;)))
В трапеции основания АД и ВС равны 36 и 12, а сумма углов при основании АД равна 90º
Найдите радиус окружности, проходящей через точки А и В и касающейся прямой СД, если АВ=10
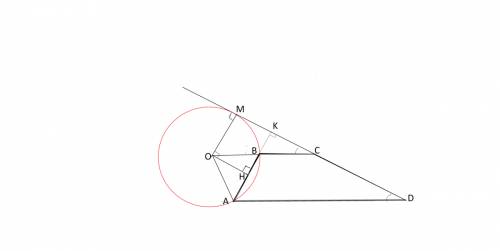
Для успешного решения задачи очень важно сделать правильный рисунок.
Из того, что сумма углов при основании АД равна 90º, следует, что продолжение АВ и СД пересекаются под углом 90º.
Достроим трапецию до прямоугольного треугольника АКД
Рассмотрим рисунок.
Не составит труда доказать, что треугольники ВКС и АКД - подобны.
∠ К в них - общий,
ВС||АД,
∠ КСВ=∠КДА по свойству углов при пересечении параллельных прямых секущей.
Коэффициент подобия АД:ВС=36:12=3
Тогда АК:ВК=3
АК=АВ+ВК
(АВ+ВК):ВК=3
(10+ВК):ВК+3
10+ВК=3ВК
2ВК=10
ВК=5
Пусть точка касания окружности и прямой СД будет М
Соединим центр О окружности с вершиной В трапеции и точкой касания М.
Так как углы ОМК и АКМ прямые, ОМ и АК - параллелльны.
Рассмотрим треугольник АОВ.
Его стороны АО и ОВ, являясь радиусами окружности, равны.
Треугольник АОВ - равнобедренный.
Проведем в нем высоту ОН.
Эта высота - и медиана ( треугольник ведь равнобедренный).
Следовательно, НВ =5.
Рассмотрим четырехугольник НКМО.
Это прямоугольник с равными сторонами НК=МО.
МО - радиус окружности.
НК=НВ+ВК=5+5=10
МО=НК=10
Радиус окружности равен 10.
Так как осевое сечение квадрат , то сторона этого квадрата и есть образующая , и также диаметр основания цилиндра. Длина образующей равна √36 = 6 , диаметр равен тоже 6 , а радиус 6:2 = 3
Площадь основания равна π R² = π · 3² = 9π
ответ образующая 6, площадь 9π