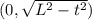. Тогда абсцисса середины отрезка x=t/2, а ордината середины 
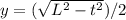. Отсюда t=2x. Подставляем это в y и получаем, что x и y связаны соотношением 
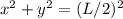. Т.е. середина отрезка описывает дугу окружности с центром в вершине прямого угла, и радиусом в половину длины отрезка.
Две стороны треугольника равны 3 и 5. Известно, что окружность, проходящая через середины этих сторон и их общую вершину, касается третьей стороны треугольника. Найдите третью сторону.
––––––––––––––––
АН и СН - касательные к окружности.
АВ - секущая, АК - её внешняя часть.
АВ=3, АК=0,5 АВ=1,5
СВ - секущая, СМ - её внешняя часть
СВ=5, СМ=СВ:2=2,5
Квадрат касательной равен произведению секущей на её внешнюю часть. ⇒
АН ²=АВ•AK=3*1,5=4,5=450/100
АН=√4,5=√(450/100)=√(9*25*2:100)=(3•5√2)/10=1,5√2
СН²=СВ•CM=5*2,5=1250/100
CH=√(25•25•2/100)=(25√2)/10=2,5√2
АС=АН+СН=1,5√2+2,5√2=4√2