Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Дано: ΔАВС, ΔА₁В₁С₁,
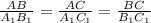
Доказать: ΔАВС подобен ΔА₁В₁С₁.
Доказательство:
На стороне АС треугольника АВС отложим СА₂ = С₁А₁ и проведем А₂В₂║АВ.
Так как прямая, параллельная стороне треугольника, отсекает треугольник, подобный данному, то
ΔАВС подобен ΔА₂В₂С , значит их стороны пропорциональны:
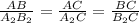 , а так как А₂С = А₁С₁, то получаем
, а так как А₂С = А₁С₁, то получаем
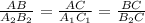 ,
,
По условию:
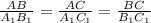 .
.
Из этих двух равенств следует, что
А₂В₂ = А₁В₁ и В₂С = В₁С₁.
Тогда ΔА₁В₁С₁ = ΔА₂В₂С по трем сторонам.
Значит,
ΔАВС подобен ΔА₁В₁С₁.
Опустим перпендикуляр CL из точки C. CL-высота. Треугольник CLD-прямоугольный. По теореме пифагора СL^2=CD^2-LD^2, CL=4. CL=AB-высота. Треугольник ABC прямоугольный. По теореме пифагора CA^2=AB^2+BC^2, CA=корень из 65. Треугольник BAD-прямоугольный. По теореме пифагора BD^2=AB^2+AD^2, BD= 2 корень из 29. Sabcd= (BC+AD)*CL/2, Sabcd=17*4/2=34. sinD=BA/CD=4/5=0,8