12 см если точка А лежит между точками С и В.
3 см если точка С лежит между точками А и В.
Объяснение:
Точки на прямой можно расположить в двух вариантах:
Первый: точка А лежит между точками С и В.
___С_4,5/_ 4,5А___7,5/___7,5В___
9 см 15 см
Тогда расстояние между серединами отрезков АВ и АС равно:
15:2 + 9:2 = 7,5 + 4,5 = 12 см.
Второй: точка С лежит между точками А и В.
Тогда расстояние между серединами отрезков АВ и АС равно:
АВ = 15 см
I7,5I - 7.5 см половина отрезка АВ
__А___4,5/I__СВ__
АС= 9 см
15:2 - 9:2 = 7,5 - 4,5 = 3 см.
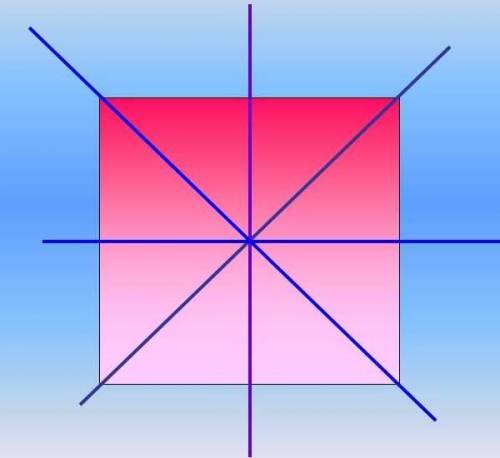
Точка О, в которой пересекаются серединные перпендикуляры, является центром квадрата, так как оба серединных перпендикуляра являются диаметрами вписанной в квадрат окружности. А диаметры пересекаются в центре окружности, т.е в точке О. Диагонали квадрата, которые являются биссектрисами, будут диаметрами описанной около квадрата окружности, которые тоже будут пересекаться в центре О. Поэтому биссектрисы квадрата и серединные перпендикуляры к сторонам квадрата пересекаются в точке О, Ч.Т.Д.
Объяснение:
256√6/3 см³
Объяснение:
Sосн=АВ²=8²=64 см² площадь квадрата.
АС=АВ√2=8√2 см.
ОС=АС:2=8√2:2=4√2 см.
tg<SCO=SO/OC
tg60°=√3
√3=SO/4√2
SO=4√2√3=4√6 см. высота пирамиды.
V=1/3*Sосн*SO=1/3*64*4√6=256√6/3 см³