Начертить одним росчерком фигуру подразумевает не проводить карандашом по одной и той же линии более одного раза. Если не соблюдать это условие, то любую из этих фигур можно нарисовать одним росчерком.
Если у фигуры есть более двух вершин с нечётным количеством рёбер, то такую фигуру одним росчерком не начертишь, потому как в каждую вершину карандаш приходит по одной линии, а уходит по другой, то есть нужно чётное количество рёбер. Исключением могут быть только крайние вершины, откуда начинается рисование, и где заканчивается рисование.
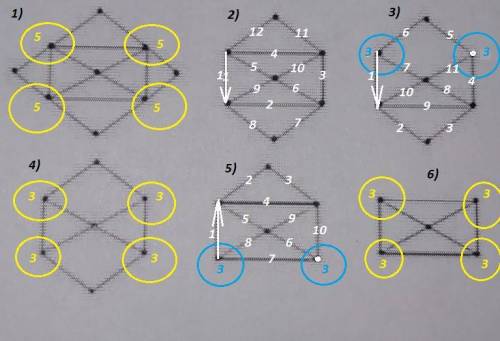
Итак, фигуры 1, 4 и 6 начертить нельзя, так как у них есть по 4 вершины с нечётным количеством рёбер.
Фигуру 2 можно нарисовать, начиная и заканчивая в одной и той же вершине.
У фигур 3 и 5 по две вершины с нечётным количеством рёбер. Начертить эти фигуры можно, начиная из одной такой вершины и заканчивая в другой аналогичной вершине.
Рисунки в приложении.
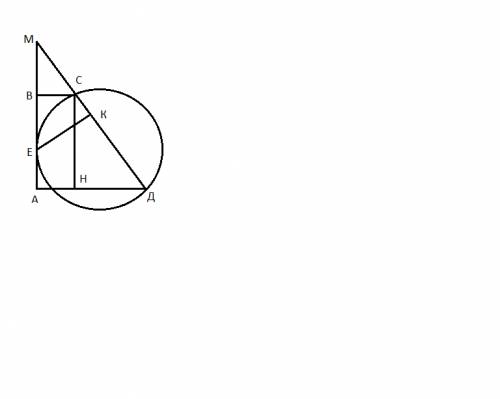
ΔKAC~ΔABC; ∠KAC > 90° ⇒ против тупого угла в ΔKAC лежит самая большая сторона CK, а в подобном ему ΔABC самая большая сторона AC=2√3 ⇒ ∠ABC = ∠ KAC > 90°
∠KCA не может быть равен ∠ACB по построению ⇒
∠KCA = ∠BAC; ∠AKC = ∠ACB ⇒
cos∠AKC = cos∠ACB
Теорема косинусов для ΔABC
AB² = AC² + CB² - 2AC*CB*cos∠ACB
√7² = (2√3)² + 1² - 2*2√3*1*cos∠ACB
7 = 13 - 4√3*cos∠ACB
4√3*cos∠ACB = 6
cos∠ACB = 6/(4√3)
cos∠ACB = √3/2 - табличный косинус ∠ACB=30°
ответ: cos∠AKC = √3/2; ∠AKC = 30°