
Утверждения 1) и 2) верные
Объяснение:
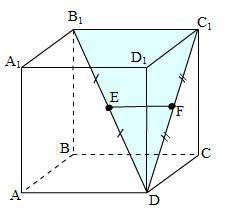
Смотри прикреплённый рисунок.
1) EF ║ B₁C₁ как средняя линия Δ DB₁C₁.
Если прямая (EF), не лежащая в плоскости (ABCD) параллельна прямой B₁C₁, лежащей в данной плоскости, то она параллельна этой плоскости. То есть EF ║ABCD или, что то же самое EF ║ABC, и утверждение 1) верное.
2) EF ║ B₁C₁ как средняя линия и B₁C₁ ║ А₁D₁ как параллельные рёбра куба. Следовательно, EF ║ А₁D₁.
Если прямая (EF), не лежащая в плоскости (AА₁D₁D) параллельна прямой A₁D₁, лежащей в данной плоскости, то она параллельна этой плоскости. То есть EF ║AА₁D₁D или, что то же самое EF ║AА₁D₁, и утверждение 2) верное.
3) EF ║ B₁C₁ как средняя линия и ребро куба B₁C₁ ⊥ плоскости грани АВВ₁А₁.
Если одна из параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости, то есть EF ⊥АВВ₁А₁ или, что то же самое EF ⊥ AА₁В₁, и утверждение 3) неверное.
4) Поскольку мы уже установили верные утверждения, то утверждение 4) неверное
HC=BC-BH=6-2=4
По т.Пифагора АС=√(АН²+НС²)= √(16+12)=2√7
Прямоугольные ∆ ВDС и ∆ АНС подобны по общему острому угу С. BC:AC=BD:AH
6:2√7=BD:2√3
BD=12√3:2√7=(6√3):√7 или (6√21):7
-------------
2) Найдем АС как в первом решении.
Площадь треугольника АВС
S=AC*BD:2
S=AH*BC:2
Т.к.площадь одной и той же фигуры, найденная любым одна и та же, приравняем полученные выражения:
AC*BD:2=AH*BC:2
(2√7)*BD:2=(2√3)*6:2
BD=(12√3):(2√7)=(6√3):√7 или (6√21):7
--
АС можно найти и по т.косинусов, а площадь ∆ АВС по формуле S=a*b*sinα:2