Для нахождения угла С в прямоугольном треугольнике АВС, мы можем использовать теорему косинусов.
Теорема косинусов гласит:
a² = b² + c² - 2bc * cos(A)
где a, b и c - длины сторон треугольника, а A - угол между сторонами b и c.
В данном случае, сторона AB длиной 32 см - это катет, сторона AC длиной 64 см - это гипотенуза, и мы ищем угол С. Таким образом, сторона BC является вторым катетом, длины которого нам неизвестны.
Мы можем применить теорему косинусов, заменяя известные значения:
64² = 32² + BC² - 2 * 32 * BC * cos(C)
4096 = 1024 + BC² - 64 * BC * cos(C)
Теперь нам нужно найти длину стороны BC и угол С. Для этого мы должны решить уравнение относительно BC и C.
4096 - 1024 = BC² - 64 * BC * cos(C)
3072 = BC² - 64 * BC * cos(C)
На данный момент мы не можем найти значение BC или С, так как нам недостаточно информации. Нам нужно еще одно уравнение, чтобы решить систему уравнений.
Давайте рассмотрим отношение между сторонами треугольника ABC. В прямоугольном треугольнике отношение катета к гипотенузе должно быть одинаковым для всех трех углов. То есть:
AB/AC = BC/AB
32/64 = BC/32
Теперь мы можем решить это уравнение относительно BC:
32 * BC = 32 * 32
BC = 32² / 32
BC = 32
Теперь, когда у нас есть значение стороны BC, мы можем вернуться к уравнению теоремы косинусов:
3072 = 32² - 64 * 32 * cos(C)
3072 = 1024 - 2048 * cos(C)
Мы можем выразить cos(C):
2048 * cos(C) = 1024 - 3072
2048 * cos(C) = -2048
cos(C) = -2048 / 2048
cos(C) = -1
Теперь, чтобы найти угол C, нам нужно найти обратный косинус (-1). Обратный косинус (-1) равен 180 градусам или пи радиан.
Таким образом, угол C = 180 градусов или пи радиан.
Ответ: Угол С в прямоугольном треугольнике АВС равен 180 градусов или пи радианам.
Медианы ЕN и FM треугольника EFK, длины которых 12 и 18, пересекаются под прямым углом. Найдите площадь Треугольника EFK.
Объяснение:
1) Рассмотрим выпуклый четырёхугольник EFNM у которого диагонали , по условию, взаимно- перпендикулярны .
Его площадь можно найти по формуле S = 1/2*d₁*d₂* sin (∠d₁d₂).
S(EFNM) = 1/2*12*18* sin 90°=108 ( ед²).
2) S(EFK)=S(EFNM)+S(MNK)
3) MN-средняя линия , тк M,N-середины сторон по определению медианы . По т. о средней линии треугольника MN║EF .
ΔEFK ∼ΔMNK по 2-м углам : ∠К -общий ,∠FEK=∠NMK как соответственные при MN║EF ,секущей ЕК ⇒ сходственные стороны
пропорциональны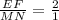
, k=
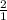. По т об отношении площадей
подобных треугольников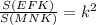
или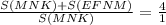 
,
4*S( MNK)=S(MNK)+S(EFNM) ,
3(MNK)=108 , S(MNK)=36 ед².
4) S(EFK)=S(EFNM)+S(MNK) =108+36=144 ( ед²).