
У нас есть 2 варианта внешнего угла — внешний угол угла, противоположному основанию, и внешний угол угла — противоположный боковой стороне.
Вариант 2-ой таков: угол, противоположный боковой стороне равен: 180-150 = 30°, в этом случае — угол, противоположный основанию равен: 180-(30+30) = 120°.
Боковая сторона равна 10, тоесть нам уже известно 2 стороны равнобедренного треугольника (боковые).
Теперь — зная их, и угол между ними (угол 120 градусов) — найдём основание по теореме Косинусов:
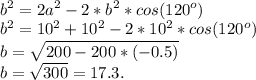
Нам известны все стороны равнобедренного треугольника.
Формула вычисления радиуса описанной окружности около равнобедренного треугольника такова:
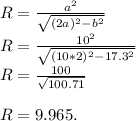
Диаметр в 2 раза больше радиуса, то есть: D = 2R = 19.93.
Вывод: D = 19.93.
Вариант 1-ый:
Внешний угол угла — противоположного основанию, тоесть: α = 180-150 = 30°.
Равные углы, противоположные боковым сторонам равняются: (180-30)/2 = 75°.
На этот раз — формула вычисления основания, зная боковую сторону, и угол между ними — будет такова:

В этом случае — радиус описанной окружности равен:
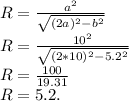
D = 2R = 5.2*2 = 10.4.
Вывод: D = 10.4.
1 .сумма смежных углов равна 180 градусов. если один из углов обозначить через х то другой х+40. х +х+40 = 180
2х +40 = 180
2х = 180 - 40
2х = 140 х=70
итак первый угол 70 градусов а другой 70*2 = 140
2. меньший угол обозначим через х тогда другой 8х.
х+ 8х = 180
9х= 180 х=20
Итак меньший угол 20 градусов, а больший 20*8=160 градусов
3.Сумма всех углов, образованных при пересечении двух прямых равна 360 градусов, значит четвёртый угол равен 360-250 = 110 градусов. Вертикальный с этим углом тоже равен 110 градусов, а ещё два угла , (они равны между собой потому, что вертикальные) равны по (250-110) : 2 =70 градусов