√2
Объяснение:
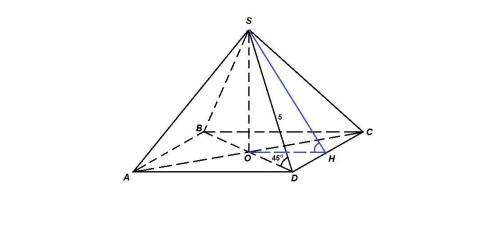
Пирамида правильная, значит в основании лежит квадрат, а боковые грани равные равнобедренные треугольники.
SO - высота пирамиды, значит DO - проекция бокового ребра SD на плоскость основания, тогда
∠SDO = 45° - угол наклона бокового ребра к плоскости основания.
Пусть Н - середина CD. тогда
SH⊥CD, так как медиана равнобедренного треугольника CSD является и высотой и
ОН⊥CD (ОН - средняя линия ΔACD, значит ОН║AD, а AD⊥CD), тогда
∠SHO - угол наклона боковой грани к плоскости основания - искомый.
______
ΔSOD: ∠SOD = 90°, ∠SDO = 45°, значит ∠OSD = 45°, треугольник равнобедренный,
SO = OD = SD / √2 = 5/√2 см
Диагонали квадрата равны, перпендикулярны и точкой пересечения делятся пополам, значит
OC = OD, ΔCOD равнобедренный, прямоугольный, CD - его гипотенуза:
CD = OD√2 = 5/√2 · √2 = 5 см
ОН = CD/2 = 2,5 см как медиана прямоугольного треугольника, проведенная к гипотенузе.
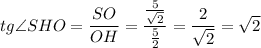
Объяснение:
1. На прямой "а" строим угол, равный 45°. На Для этого на прямой отмечаем точку А и проводим через нее прямую "b", перпендикулярную прямой "а". Проводим полуокружность из центра А произвольного радиуса и в местах пересечения этой полуокружности с прямыми "а" и "b" отмечаем точки В и С соответственно. Соединяем точки В с С отрезком. Угол СВА равен 45°. Угол СВК равен 180 - 45 = 135° (точку К отмечаем на прямой "а" в любом месте левее точки В => углы СВК и СВА - смежные).
2. Считаем, что Вы умеете строить угол, равный данному.
Строим угол, равный 30°. Для этого проводим вертикальную прямую "а" и отмечаем на ней точку А. Из точки А как из центра проводим полуокружность до пересечения с прямой "а" в точку В. Этим же радиусом проводим полуокружность с центром в точке В и в местах пересечения полуокружностей отмечаем точки C и D. Соединяем точки А,В и С. Угол АСD равен 30°, так как треугольник АВС равносторонний, а CD - биссектриса угла АВС (CD⊥AC).
Теперь на стороне СD строим угол DCE, равный данному. То есть ∠DCE = 35°. Следовательно, ∠АСЕ = 5°.
На прямой СА строим угол FСG, равный данному углу АСЕ.
Повторяем эту процедуру 5 раз. Полученные углы ECF, FCG, GCH, HCI, ICJ, JCK и KCD равны по 5°, то есть мы разделили угол ECD на 7 равных частей.