Ромб - стороны равны, противоположные углы равны, диагонали перпендикулярны.
Треугольники ABE и CBF равны по гипотенузе и острому углу, AE=CF.
Точки E и F делят стороны ромба в равном отношении => AC||EF => EF⊥BD
S(ABO) =1/4 S(ABCD) =1/4 *1/2 *160*120 =2400
AB =√(AO^2 +BO^2) =100
∠ABD=∠ADB => △ABO~△BDE
BE/AO =BD/AB => BE =80*120/100 =96
△BEG~△BMO~△BDE => △BEG~△BMO~△ABO
S(BEG)/S(ABO) =(BE/AB)^2 =(96/100)^2 =0,96^2
S(BMO)/S(ABO) =(BO/AO)^2 =(60/80)^2 =0,75^2
S(MOGE) =S(BEG)-S(BMO) =2400 (0,96^2 -0,75^2) =861,84
S(MNFE) =2 S(MOGE) =1723,68
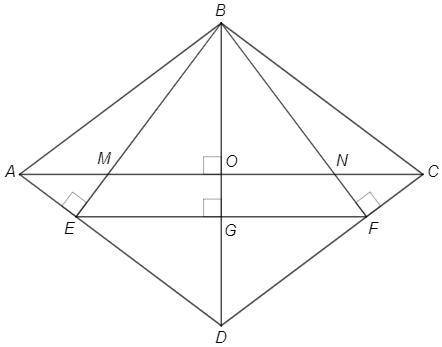
На самом деле плоскость проходит не через С, а через B и N. На рисунке она правильно изображена. Плоскость АМС сечение пересекает по прямой, параллельной АС. Отсюда сразу следует, что (если обозначить К точку пересечения МА и сечения), что поскольку KN II AC, АК/КС = CN/NM = 1/2;
Поэтому, во первых, KN = АC*2/3) (из подобия треугольников АМС и MKN), и - во вторых, (если обозначить Р - точку пересечения высоты пирамиды МО и сечения) МР/РО = 2/1, то есть Р - точка пересечения медиан треугольника MBD. То есть прямая ВР, лежащая в плоскости сечения - это медиана треугольника MBD. То есть сечение делит MD пополам (надо еще обозначить Q - середина MD).
Легко видеть, что KN перпендикулярно плоскости MBD (обоснование! - самостоятельно), то есть KN перпендикулярно BQ. Таким образом, в четырехугольнике BKQN, который получается в сечении, диагонали KN и BQ взаимно перпендикулярны.
Площадь BKQN равна половине произведения диагоналей, S = KN*BQ/2; KN = 2√2/3; осталось найти BQ.
BQ - медиана в равнобедренном треугольнике BMD со сторонами BM = MD =2; BD = √2;
(2*BQ)^2 = 2*(BD)^2 + MD^2 = 8; BQ = √2; (занятно, что треугольник BQD подобен треугольнику MBD);
S = √2*(2√2/3)/2 = 2/3.