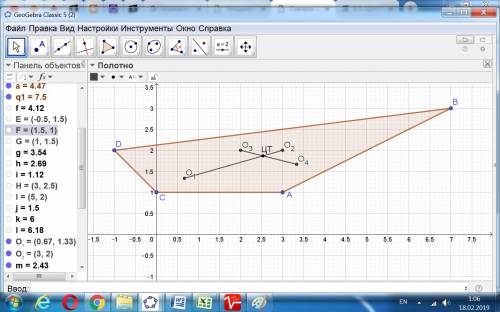
Сначала делим четырехугольник диагональю на два треугольника.
Находим центр тяжести каждого треугольника как точку пересечения его медиан. Центр тяжести четырехугольника лежит на прямой О1О2, соединяющей центры тяжести этих треугольников.
Затем делим четырёхугольник на 2 треугольника при другой диагонали и находим так же центры тяжести других треугольников. Соединяем их отрезком О3О4.
Искомый центр тяжести четырёхугольника лежит в точке ЦТ пересечения отрезков О1О2 и О3О4.
ABD x y BCD x y
O2 3 2 O3 2 2
ADC x y ABC x y
O1 0,6667 1,3333 O4 3,3333 1,6667
ЦТ = х у
2,533 1,8667
Объяснение:
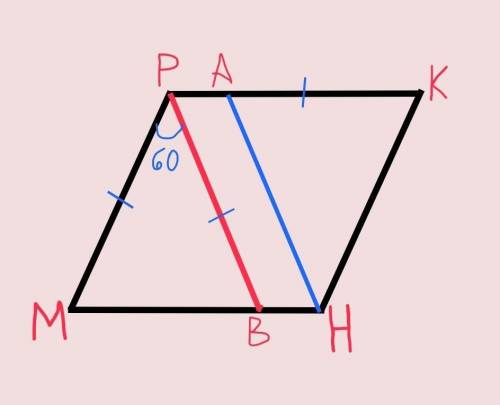
Так как МР=РВ по условию, то ∆МРВ – равнобедренный. Углы при основании равнобедренного треугольника равны, а сумма всех углов равна 180°.
Тогда угол PMB=угол РВМ=(180°–МРВ)÷2=(180°–60°)÷2=60°.
Получим что все углы ∆МРВ равны 60°, тогда ∆МРВ – равносторонний.
Тогда МВ=МР.
Углы при одной стороне параллелограмма в сумме равны 180°.
Значит угол МРК=180°–угол РМВ=180°–60°=120°
Противоположные углы параллелограмма равны.
Следовательно угол РКН=угол РМН=60°; угол МНК=угол МРК=120°.
МР=АК по условию
МР=КН так как противоположные стороны параллелограмма равны.
Углы при основании равнобедренного треугольника равны, а сумма всех углов равна 180°.
Следовательно: угол КАН=угол КНА=(180°–угол АКН)÷2=(180°–60°)÷2=60°.
Получим что все углы ∆АКН равны 60°, тогда ∆АКН – равносторонний. Исходя из этого АН=АК
МВ=МР=АК=АН => МВ=АН.
ответ: 1) 60°; 120; 2) равны.
Очень много раз эта задача тут выложена, я делаю в последний раз.
Пусть b=24; a = 12; О - центр основания, МО - высота пирамиды, сечение пересекает MD в точке Q, МС в точке Р, МО в точке К. Надо найти площадь четырехугольника BGQP.
Плоскость сечения II АС, поэтому GP II AC, откуда MG/GA = МК/КО = MP/PC = 2/1;
то есть
1. GP = (2/3)*AC = a*2√2/3; (из подобия треугольников AMC и GMP)
2. К - точка пересечения медиан треугольника MDB. То есть MQ = DQ;
И еще, поскольку у квадрата диагонали перпендикулярны, AC перпендикулярно плоскости треугольника MDB, откуда следует, что GP перпендикулярно BQ, то есть площадь S четырехугольника BGQP равна S = BQ*GP/2;
Остается найти медиану m = BQ равнобедренно треугольника MDB с боковыми сторонами MD = MB = b = 24; и основанием BD = a√2; (a = 12);
(2*m)^2 = 2(a√2)^2 + b^2;
m = (1/2)*√(4*a^2 + b^2);
S = (1/2)*(a*2√2/3)*(1/2)*√(4*a^2 + b^2) = (1/6)*a*√(8*a^2 + 2*b^2);
ну и надо подставить числа.
если b = 2*a, то S = (2/3)*a^2 = 96;