Любые две из трех прямых, соединяющих середины отрезков AB и CD; AC и BD; AD и BC могут быть:
а) параллельны одной из этих прямых.
Через две параллельные прямые можно провести плоскость, притом только одну.
б) пересекаться:
Через две пересекающиеся прямые можно провести плоскость, притом только одну.
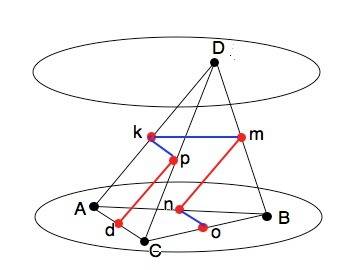
В рисунке приложения даны некоторые из получающихся пар параллельных и пересекающихся прямых:
а) pd и mn как средние линии треугольников АСD и BCD параллельны AD; kp и no параллельны основанию АС треугольников АDC и АВС.
б) km и mn, mn и no пересекаются.
Вершина прямого угла - точка А. От А вверх 12 см (точка В), от А в сторону 16 см (точка Д), от Д вверх 12см (точка С). соединить точки В и С. Получили прямоугольник АВСД. Проведем диагональ АС, её и надо найти.Рассмотрим треугольник АСД - он прямоугольный. По теореме Пифагора находим гипотенузу АС. АС квадрат = АД квадрат+ СД квадрат. АС квадрат= 16 квадрат+12 квадрат, АС квадрат=256+144=400. АС = 20 (см)