nima bu jora qolaysan uka
№1. Из условия видим, что диагональ BD делит ромб на два правильные треугольника ABD и CBD. Можно по теоремме пифагора найти высоту этих треуг-ков, а затем их площадь, но для равностороннего треуг-ка есть такая формула площади:
S=(√3/4)*a^2
S=√3/4*10=2√3/5=0,7см^2
№2. Сторона правильного шестиугольника равна радиусу описанной около него окружности, поэтому r=6см.
Длина окр-ти l=2Пr=2*3,14*6=37,68см
S=Пr^2=3,14*36=113,04см^2
№3. Что-то не понял условие. Дан прямоугольный треугольник и найти радиус вписанного треугольника. Радиус вписанной окружности нужно найти.
r=S/p, где р-полупериметр. Так как острый угол 45, то катеты равны.
Пусть один катет равен х, тогда
x^2+x^2=100
2x^2=100
x^2=50
x=√50=5√2см
S=1/2*5√2*10=25√2см^2
p=(10+5√2+5√2)/2=5+5√2см
r=25√2/(5+5√2)=5√2/(1+√2)=2,93см
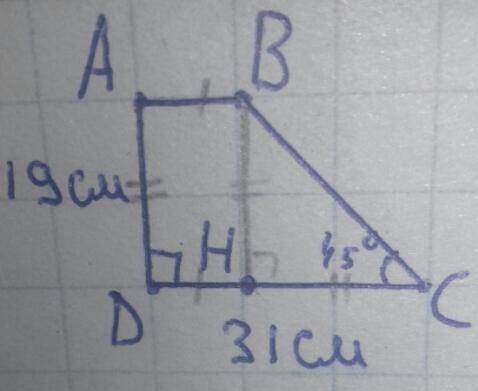
Вступление:
Пусть в прямоугольной трапеции ABCD, AB и CD основания, а ∠D прямой. Тогда AD меньшая боковая сторона (как расстояние между параллельными отрезками AB и CD), то есть AD=19см. По построению DC большое основание, поэтому по условию DC=31см. Острые углы при большом основании, ∠C=45° т.к. ∠D=90°.
H∈DC, BH⊥DC ⇒ BH=AD=19см.
В прямоугольном ΔBHC:
∠C=45°, ∠H=90° ⇒ ∠B=45°⇒ HC=BH=19см.
DH=DC-HC=31-19=12см.
В четырёхугольнике ABHD:
∠D=90°, ∠H=90° и ∠A=90°, ∠B=90° т.к. AB║DH, ведь H∈DC и AB║DC.
Получается ABHD - прямоугольник, поэтому AB=HD, HD=12см ⇒ AB=12см.
AB мень. осн. т.к. CD - большее.
Меньшее основание равно 12см.
Биссектриса делит угол пополам, т.е. ∠ABD = ∠DBC; ∠BAD=∠DAC.
1) \sf \angle \,BAD=\frac{1}{2}\angle\, A=\frac{1}{2}\cdot 50^\circ=25^\circ∠BAD=21∠A=21⋅50∘=25∘
\sf \angle\, ABD=\frac{1}{2}\angle \, B=\frac{1}{2}\cdot100^\circ=50^\circ∠ABD=21∠B=21⋅100∘=50∘
И рассмотрим треугольник ABD в нем сумма углов должна быть равна 180°,т.е. \sf \angle \,ADB=180^\circ-25^\circ-50^\circ=105^\circ∠ADB=180∘−25∘−50∘=105∘
2) Аналогично с примером 1)
\sf \angle \,BAD=\frac{1}{2}\angle\, A=\frac{1}{2}\cdot \alpha=\frac{\alpha}{2}∠BAD=21∠A=21⋅α=2α
\sf \angle\, ABD=\frac{1}{2}\angle \, B=\frac{1}{2}\cdot\beta=\frac{\beta}{2}∠ABD=21∠B=21⋅β=2β
\sf \angle \,ADB=180^\circ-\frac{\alpha}{2}-\frac{\beta}{2}=180^\circ-\frac{1}{2}(\alpha+\beta)∠ADB=180∘−2α−2β=180∘−21(α+β)
3) Сумма углов треугольника ABC равна 180°, т.е. ∠A+∠B+∠C=180°.
∠A + ∠B + 130° = 180°
∠A + ∠B = 180° - 130°
∠A + ∠B = 50°
∠ADB = 180° - 1/2(∠A + ∠B) = 180° - 1/2 * 50° = 180° - 25° = 155°
4) Аналогично с примером 3)
∠A + ∠B + ∠C = 180°
∠A + ∠B + \gammaγ = 180°
\sf \angle\, A+\angle \, B=180^\circ-\gamma∠A+∠B=180∘−γ
Тогда
\begin{gathered}\sf \angle\, ADB=180^\circ-\frac{1}{2}(\angle \, A+\angle \, B)=180^\circ-\frac{1}{2}(180^\circ-\gamma)=180^\circ-90^\circ+\frac{\gamma}{2}=\\ \\ =90^\circ+\frac{\gamma}{2}\end{gathered}∠ADB=180∘−21(∠A+∠B)=180∘−21(180∘−γ)=180∘−90∘+2γ==90∘+2γ