43
Объяснение:
Число пересечений не параллельных прямых можно представить в виде прогрессии. Где N - число прямых. Аn это N-й член прогрессии или число пересечений N прямых. Тогда Аn = Аn-1 + (N - 1), где Аn-1 - предыдущий член прогрессии. (N - 1) это, как постоянный член арифметической прогрессии, но здесь он меняется, поэтому найти любой член формулами арифметической прогрессии у меня пока не получается, но можно посчитать вручную или забить формулу в Exel. Например для 2х прямых формула принимает вид 0+2-1=1 и т. д. Для десяти прямых - 45 пересечений.
Теперь три прямых, которые пересекаются в 1й точке теряют 2 пересечения. Это число нужно вычесть из общей суммы.
Дано :
ΔАВС — прямоугольный (∠В = 90°).
АВ = 5, ВС = 7.
Найти :
АС = ?
∠А = ? ; ∠С = ?
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы (теорема Пифагора).Следовательно, АС² = АВ² + ВС² = 5² + 7² = 25 + 49 = 74 ⇒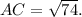
Найдём тангенс ∠А (отношение противолежащего катета — ВС к прилежащему катету — АВ) :
В таблице Брадиса это примерное значение тангенса острого угла в 55°.
Тогда второй острый угол прямоугольного ΔАВС — ∠В = 90° - ∠А ≈ 90° - 55° ≈ 35°.