Вложение:))))))))))))))))))))))))))))))))))))))))

W, V - центры
Проведем WK⊥AE, VL⊥AE
BK=1, DL=1 (перпендикуляр из центра к хорде делит ее пополам)
AK=3, AL=6
Проведем WN⊥VL
Понятно, что W - середина AV, N - середина VL
WK=VN=NL=x
Rw =WB =√(WK^2+BK^2) =√(x^2+1)
Rv =VD =√(VL^2+DL^2) =√(4x^2+1)
WV =Rw+Rv (точка касания лежит на линии центров)
WV =√(VN^2+WN^2) => Rw+Rv =√(x^2+9)
√(x^2+1) + √(4x^2+1) = √(x^2+9)
x^2 +1 +4x^2 +1 +2√(x^2+1)√(4x^2+1) = x^2 +9
4(x^2+1)(4x^2+1) = (7-4x^2)^2 // при 7-4x^2 >=0 => x<=√7/2
16x^4 +16x^2 +4x^2 +4 = 49 -56x^2 +16x^4
76x^2 = 45 => x=√(45/76)
Rw =√(45/76 +1) =√(121/76) =11/2√19
Rv =√(4*45/76 +1) =√(256/76) =8/√19
Основанием пирамиды является равнобедренный треугольник с углом α при основании и радиусом вписанной окружности г. Две боковые грани пирамиды, содержащие боковые стороны основания, перпендикулярны плоскости основания, а третья - наклонена к ней под углом β. Найдите объём пирамиды.
Объяснение: V(пир.)=1/3*S(основания)*h , h- высота пирамиды.
1) Найдем S(основания)=S(ΔАВС)=1/2*АС*ВН=АН*ВН.
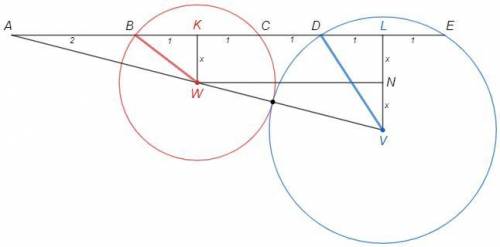
Из ΔАВН ,угол ∠АВН=90°-α. По свойству касательной ОР⊥АВ, ОР=r ,Тогда из ΔВРО-прямоугольного 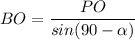 или
или 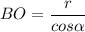 .
.
Высота ВН=ВО+ОН , 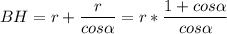 .
.
Из ΔАОН ,найдем АН. Тк АО-биссектриса , то ∠ОАН=α/2 ⇒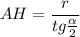 .
.
S(ΔАВС)=АН*ВН=  .
.
2) Т.к две боковые грани пирамиды, содержащие боковые стороны основания, перпендикулярны плоскости основания , то линия пересечения , отрезок МВ⊥(АВС)⇒ МВ-высота пирамиды..
Т.к ВН⊥АС , то и наклонная МН⊥АС по т. о трех перпендикулярах.Тогда углом между плоскостями (АВС) и ((АМС) будет линейный угол ∠ВНМ=β.
ΔМВН-прямоугольный , ,
,
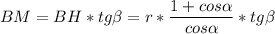 ,
, 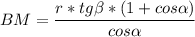 .
.
3)Обьем 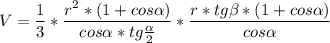 ,
,
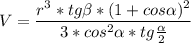 .
.

Если внешний 130, то угол АВС=50, 180-50=130 (по теореме о сумме углов треугольника) В равнобедренном треугольнике углы при основании равны, соответственно 130/2=65.