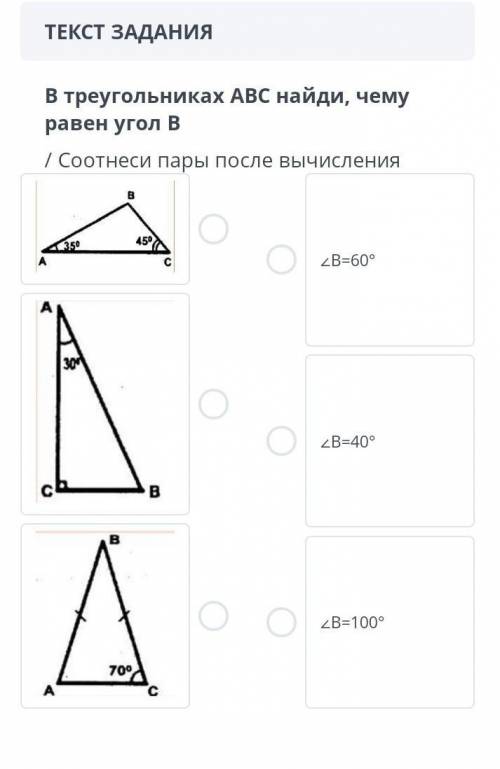
1— <В=100°( <А=35°; <С=45°)
2— <В=60° ( <А=30°; <С=90°)
3— <В=40° (<А=70°; <С=70°)
Объяснение:
∆—180° ↓
1—180°-(35°+45°)=100°
2—180°-(30°+90°)=60°
3—180°-(70°+70°)=40°
ответ: рассматриваем равновесие точки с, которая считается несвободной, так как на нее наложены связи в виде стержней ас и вс. освобождаем точку с от связей и заменяем их силами реакций связей, считая, что стержень ас растягивается, а стержень вс сжимается под действием силы f. обозначим реакцию стержня ас через n1, а реакцию стержня вс через n2. в итоге точка с становится свободной, находясь под действием плоской системы трех сходящихся сил: активной силы f и сил реакций n1 и n2 (рис. 1, б). приняв точку о за начало координат, перенесем силы f, n1 и n2 параллельно самим себе в эту точку (рис. 1, в) и составляем уравнения проекций сил на оси координат:
или
(1)
и
. (2)
умножим уравнение (1) на , получим
(3)
. (4)
после сложения уравнений (3) и (4) получим
откуда 2n2 = f или н. из уравнения (1) получаем, что
или н.
графический метод. для решения этим методом выбираем масштаб силы f (например, 10 н = 1 мм) и строим замкнутый треугольник сил (рис. 1, г). из произвольной точки о проводим прямую, параллельную вектору f, и откладываем на этой прямой в выбранном масштабе вектор . из конца вектора (точка а) проводим прямую, параллельную вектору , а из точки о — прямую, параллельную вектору . пересечение этих прямых дает точку в. получили замкнутый треугольник сил оав, стороны которого в выбранном масштабе изображают силы, сходящиеся в точке с. величины сил n1и n2 определим после измерения сторон ав и во треугольника оав.
объяснение:
Номер 1
<В=180-(35+45)=180-80=100 градусов
Номер 2
Треугольник прямоугольный
<В=180-(90+30)=180-120=60 градусов
Номер 3
Треугольник равнобедренный,углы при основании равнобедренных треугольников равны между собой
<А=<С=70 градусов
<В=180-70•2=40 градусов
Объяснение: