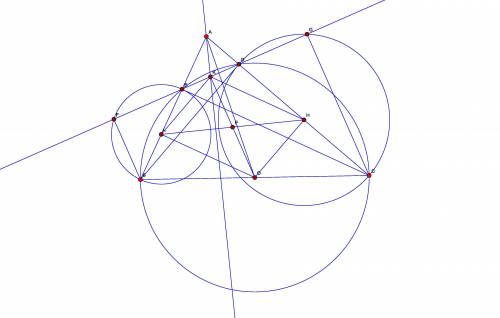
См. чертеж.
Построенные окружности "демонстрируют" скрытые связи, которые есть в конструкции. Если их мысленно убрать, получится построение из условия задачи.
Так как EC перпендикулярно AB, точка Е лежит на окружности. построенной на BC, как на диаметре, и центром этой окружности будет середина BC - точка O. Точно также - точка D. Аналогично, L - середина BE, H - середина CD.
Первое. Я собираюсь доказать, что FE = DG; но делать я это буду "через Китай". Пусть точка K - середина ED. Если удастся доказать, что K лежит на радикальной оси окружностей (BFE) и (DGC), то из этого автоматически будет следовать FE = DG
Про радикальную ось этих окружностей известно две вещи. Во-первых, она перпендикулярна линии центров LH; во-вторых, она проходит через точку A, поскольку точка A - радикальный центр всех трех окружностей, изображенных на чертеже. В самом деле, AB и AC - радикальные оси пар окружностей (BFE) (BCED) и (DGC) (BCDE), а значит, их общая точка имеет равные степени относительно (BFE) и (DGC) (я повторил доказательство теоремы о радикальном центре).
Таким образом, задача свелась к тому, что надо доказать перпендикулярность AK и LH.
Треугольники ADE и ABC подобны, => AO и AK - соответствующие медианы в подобных треугольниках (я пока не знаю, понадобится ли это для решения).
Четырехугольник KHOL - параллелограмм Вариньона для четырехугольника BEDC; его стороны параллельны BD и CE и равны их половинам. => ∠KHO = ∠BAC; (стороны этих углов взаимно перпендикулярны) кроме того, KH = CE/2 = AC*sin(A)/2; HO = BD/2 = AB*sin(A)/2; то есть треугольники ABC и KHO подобны с коэффициентом sin(A)/2; => треугольник KHO подобен треугольнику EAD, Стороны их одинаково ориентированы (см чертеж, например, ясно, что при повороте на "минус" 90°, то есть по часовой стрелке, и каком-то сдвиге и сжатии, соответствующие стороны переходят друг в друга, EA -> KH; AD -> HO;) => существует поворотная гомотетия, переводящая EAD -> KHO, при этом угол поворота равен 90°, поскольку стороны взаимно перпендикулярны. Ясно, что при этом AK -> HP (Р - точка пересечения диагоналей параллелограмма KHOL, и => середина KO и HL); поэтому AK перпендикулярно HP чтд.
Итак, K лежит на радикальной оси окружностей (BFE) и (DGC), и поскольку KE = KD, EF = DG; (в переводе на "человеческий" язык это означает вот что - у точки K - середины DE, - равны степени относительно этих окружностей, то есть KG*KD = KF*KE; поскольку KE = KD, KF = KG; => EF = DG;)
по условию FG = 7; DE = 3; => EF = DG = 2;
См. Объяснение
Объяснение:
Стандартные размеры винтовой лестницы (если позволяет место, где эта лестница монтируется):
1) Наружный диаметр = ширина лестничного марша (без учёта диаметра внутреннего столба) х 2 =
60 · 2 = 120 см - минимум;
95 · 2 = 190 см - максимум.
2) Внутренний диаметр (диаметр столба) - 15 см;
3) Стандартный шаг винта, или высота подъёма на 1 оборот = 2,2 м.
4) Высота подступенка (шаг между одноименными точками ступеней) - 20 см (шаг включает толщину ступени; если ступени из дерева, то их высота должна быть порядка 5 см, или ≈2 дюйма); чем меньше высота подступенка, тем легче подниматься по лестнице.
РАСЧЕТ
1) Угол поворота.
За 1 полный оборот мы поднимемся вверх на 2,2 м. Останется подняться ещё на:
3 - 2,2 = 0,8 м.
Пересчитаем 0,8 м высоты в градусы поворота:
0,8 : 2,2 · 360 = 131°
Значит, при подъёме на 3 м мы повернём в итоге на:
360 + 131 = 491°- то есть точка выхода с лестницы будет не над точкой входа, а за ней - на расстоянии чуть больше 1/3 окружности.
2) Количество ступеней:
3000 мм (высота подъёма) : 200 мм (высота подступенка) = 15 ступеней.
пусть SO высота, SA образующая, ОА радиус основания
Треуг. SOA прямоугольный, угол SAO=a, тогда Cos a=OA/SA, OA=12*cos a, a=45, значит ОА=12*sqrt(2)/2=6*sqrt(2)
Sоснования=pR^2=p*36*2=72p