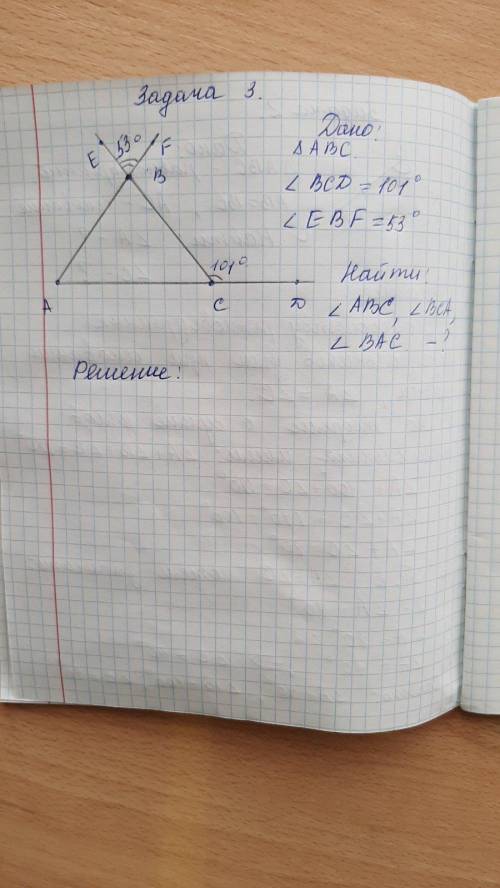
Т.к. угол ВСD и угол BCA - смежные, то угол BCD + BCA = 180°, следовательно угол ВСА = 80°. 2) Т.к. треугольник АВС - равнобедренный, то угол А = ВСА = 80°. 3) По теореме о сумме углов треугольника угол А+В+ВСА = 180°, значит. В = 180° - (80°+80°) = 180° - 160° = 20°. ответ: 80°, 20°, 80°. Новые вопросы в Геометрия. Дано : ABC, AB= BC LKBA =100 Внешний угол Найти : LA, LC
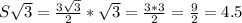
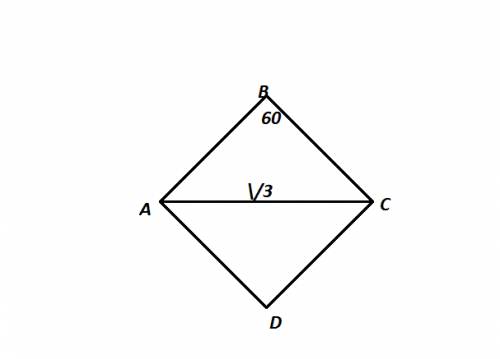
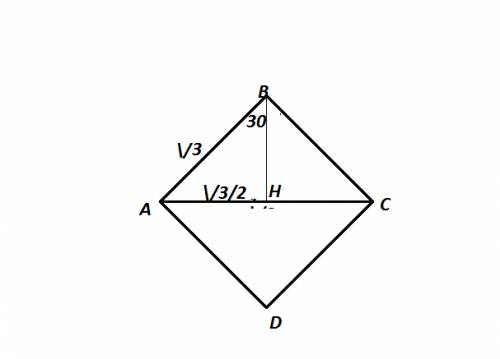
угол АВС 53° , угол ВАС 79°