Это достаточно просто. Признак равенства треугольников по двум сторонам и углу между ними можно использовать.
Треугольник ABC с медианами AK BL CM и треугольник DEF с медианами DO EP FR.
Так как треугольники равны, AB=DE BC=EF AC=DF, в силу свойств медианы половины равных сторон также равны BK=KC = EO=OF, углы a=d b=e c=f.
Получаем для ABK и DEO
AB=DE по условию
BK=EO
a=d по условию. Эти треугольники равны, соответственно и равны все их стороны.
То же самое верно для двух оставшихся медиан.
Что и требовалось доказать.
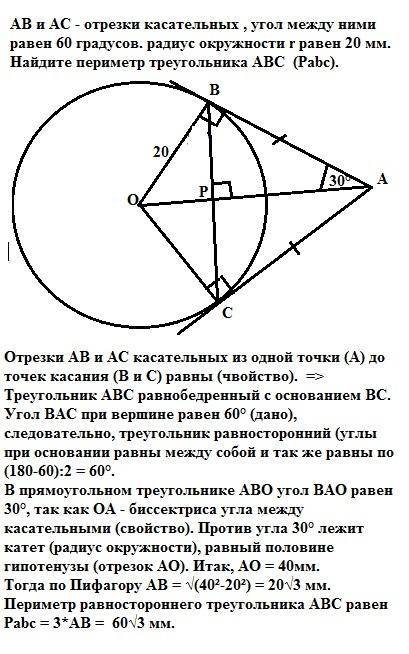
Отрезки АВ и АС касательных из одной точки (А) до точек касания (В и С) равны (свойство). =>
Треугольник АВС равнобедренный с основанием ВС.
Угол ВАС при вершине равен 60° (дано), следовательно, треугольник равносторонний (углы при основании равны между собой и так же равны по (180-60):2 = 60°.
В прямоугольном треугольнике АВО угол ВАО равен 30°, так как ОА - биссектриса угла между касательными к окружности (свойство). Против угла 30° лежит катет (радиус окружности), равный половине гипотенузы (отрезок АО). Итак, АО = 40мм.
Тогда в треугольнике АОВ по Пифагору АВ = √(40²-20²) = 20√3 мм.
Периметр равностороннего треугольника АВС равен
Pabc = 3*АВ = 60√3 мм.
1)AB^2=AO^2+BO^2-2*AO*BO*cosAOB, получаем
AB^2=4+3-2*2*под корнем 3*под корнем3/2=7-2*3под корн.*3под корн.=7-6=1,
тогда получим что AB=1
S(OCH)=1/2AC*BD*sinAOB=1/2*4*3под корн.*1/2=2под корн.3, уточняю что угол AOB=30град., а угол BOC=150град., то получается что OE=1 высота пирамиды.
V=1/3S(OCH)*h=1/3*2под корн.3*1=2под3/3
V=2*3под корн./3.
3)
R= 7, L=10.Sос сеч=?, Sпов=?, V=?
Soc=1/2 * 14 * 10=70
Sпов=ПR(R+L)=П*7(7+10)=119П
4)
a=7, b=9. Sпов=?
Sпов=2*П*7*(7+9)=224П
7)
Ребро DA перпендикулярно к плоскости АВС , а плоскость DBC составляет с плоскостью АВС угол 30*.
Найдите площадь боковой поверхности пирамиды.
S(бок) = 2S(АДС) + S(ВСД)
Угол ДКА = 30, тогда АД = АК* tg30 = (aV3/2)*V3/3 =a/2
Тогда S(АСД) = 1/2*а*а/2 = а^2 / 4
ДК = а, тогда S(ВСД) = 1/2*а*а = а^2 / 2
S(бок) = 2*(а^2 / 4) * (а^2 / 2) = а^2.