Дано :
AB ∩ CD = O.
AO = 12 см.
ВО = 4 см.
СО = 30 см.
DO = 10 см.
∠DOB = 52°.
∠DBO = 61°.
Найти :
∠АСО = ?
∠АОС = ∠DOB - как вертикальные.
Теперь проверим следующее отношение -
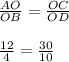
Отношение верно, следовательно, ΔАОС ~ ΔBOD по двум пропорциональным сторонам и равному углу между ними (второй признак подобия треугольников).
Рассмотрим ΔBOD.
По теореме о сумме углов треугольника -
∠В + ∠О + ∠D = 180°
∠D = 180° - ∠В - ∠О = 180° - 61° - 52° = 67°.
Причём стороны АО и ОВ - сходственные (стороны в подобных треугольниках, лежащие напротив равных углов).
Тогда получаем, что -
∠D = ∠ACO = 67°.
67°.

Пусть х см - пятая часть меньшего катета, тогда 5х - длина меньшего катета, 12х - длина большего катета. Так как по теореме Пифагора гипотенуза^2 = меньший катет^2+больший катет^2, составляем уравнение: 39^2 = (5x)^2+(12x)^2; 1521 = 25x^2+144x^2; 1521 = 169x^2; x^2 = 1521/169; x^2 = 9; x = 3; 5x = 15 - длина меньшего катета. ответ: 15.