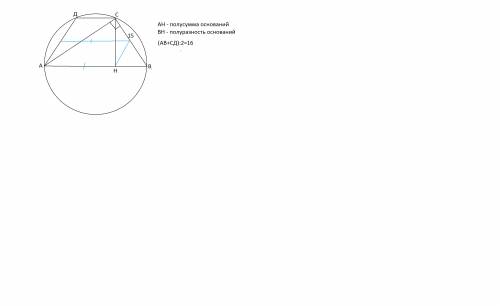
⊿ АВС - прямоугольный, т.к. его вершины лежат на окружности, а большая сторона - диаметр этой описанной окружности.
СН- высота этого треугольника и высота трапеции.
По свойству высоты прямоугольного треугольника к гипотенузе
катет прямоугольного треугольника есть среднее пропорциональное между
гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой.
СВ² =ВН∙АВ
Полусумма оснований трапеции ( средняя ее линия) =16 см, ⇒АВ+СД=32 см
Для удобства вычислений обозначим длину
СД=х
Тогда АВ=32-х,
ВН=(32-х-х):2=16-х
Из ⊿ВСН по теореме Пифагора найдем величину х.
Для этого подставим в уравнение СВ² =ВН∙АВ обозначения каждой стороны.
Получим квадратное уравнение
х² - 48х + 287=0
Корни этого уравнения равны 7 и 41( 41 не подходит, т.к. меньшее основание трапеции не может быть больше средней линии)
х=7 см ( это длина меньшего основания трапеции)
Дальнейшие вычисления дают нам высоту трапеции ВН= 12 см
S трапеции=12∙16=192 см²
АД перпендикулярно ВС угол АДС = 90 градусов и угол АДВ равен 90 градусов
Рассмотрим треугольник АДС он прямоугольный и равнобедренный т.к. угол С = 45 градусов, а угол АДС = 90 градусов следовательно угол САД = 45 градусов, а против равных углов лежат равные стороны, следю АД=ДС=8см.
Sтреуг = а*в/2 следовательно площадь треугольника АДВ =8*6/2=24 см
а площадь треугольника АДС = 8*8/2 = 32 см. Площадь треуг АВС равна 32 + 24=56 см.
ответ: Высота АД = 8 см.
Плошадь треугольника АВС = 56 см.