Объяснение:
Синус кута - це відношення протилежного катета до гіпотенузи,
Косинус кута - це відношення прилеглого катета до гіпотенузи,
Тангенс кута - це відношення протилежного катета до прилеглого катету.
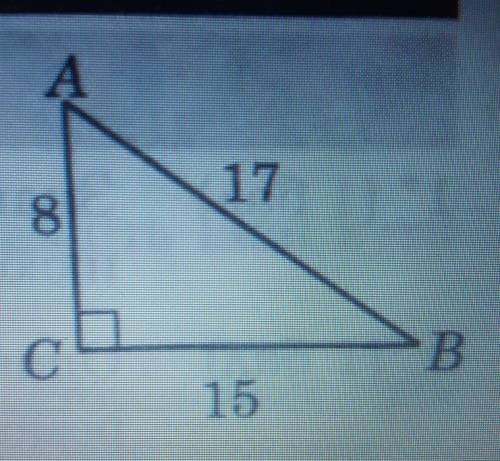
На цей раз, що sin A= 15/17 ; cos B= 15/17 ; tg A= 15/8 ; sin B=8/17
Отрезок BD - диаметр окружности с центром О. Хорда AC делит
пополам радиус OB и перпендикулярна к нему. Найдите углы
четырёхугольника ABCD и градусные меры дуг AB BC CD и AD.
Соединим центр окружности с вершиной А.
Отрезок ОА - радиус, МО равен его половине.
sin ∠ МАО равен МО: АО=1/2.
Это синус 30°∠ МАО=30°, ⇒∠ АОВ=60°.
ВО=АО=радиус окружности. ⇒ △ АОВ равнобедренный.
Сумма углов треугольника 180 градусов.
∠ ОВА=∠ОАВ=(180°-60°):2)=60° ⇒ △ АОВ- равносторонний.
Углы ВАD и ВСD опираются на диаметр ⇒ они прямые=90°.
⊿ ВСD и ⊿ВАD -прямоугольные, и
∠СDВ=∠АDВ=180°-(90°-60°)=30°
⊿ ВСD=⊿ВАD.
∠ D=2 ·∠АDВ=2·30°=60°
Сумма углов четырехугольника 360°
∠АВС=360°- 2·90°- 60°=120°
Градусная мера дуги равна центральному углу, который на нее
опирается.
На дугу АВ опирается центральный угол АОВ=60°⇒ ее градусная мера 60°
На дугу СВ опирается центральный угол СОВ=60°⇒ ее градусная мера 60°
В треугольнике САD ∠САD=∠DАС=60°
Вписанный угол равен половине градусной меры дуги, на которую
опирается.
На дугу CD опирается вписанный угол САD=60°⇒ она равна 2·60°=120°
На дугу АD опирается вписанный угол АСD=60°⇒ она равна 2·60°=120°
∠А=С=90°
∠В=120°
∠Д=60°
градусные меры дуг
AB=60°
BC=60°
CD=120°
AD=120°.
Отрезок BD - диаметр окружности с центром О. Хорда AC делит
пополам радиус OB и перпендикулярна к нему. Найдите углы
четырёхугольника ABCD и градусные меры дуг AB BC CD и AD.
Соединим центр окружности с вершиной А.
Отрезок ОА - радиус, МО равен его половине.
sin ∠ МАО равен МО: АО=1/2.
Это синус 30°∠ МАО=30°, ⇒∠ АОВ=60°.
ВО=АО=радиус окружности. ⇒ △ АОВ равнобедренный.
Сумма углов треугольника 180 градусов.
∠ ОВА=∠ОАВ=(180°-60°):2)=60° ⇒ △ АОВ- равносторонний.
Углы ВАD и ВСD опираются на диаметр ⇒ они прямые=90°.
⊿ ВСD и ⊿ВАD -прямоугольные, и
∠СDВ=∠АDВ=180°-(90°-60°)=30°
⊿ ВСD=⊿ВАD.
∠ D=2 ·∠АDВ=2·30°=60°
Сумма углов четырехугольника 360°
∠АВС=360°- 2·90°- 60°=120°
Градусная мера дуги равна центральному углу, который на нее
опирается.
На дугу АВ опирается центральный угол АОВ=60°⇒ ее градусная мера 60°
На дугу СВ опирается центральный угол СОВ=60°⇒ ее градусная мера 60°
В треугольнике САD ∠САD=∠DАС=60°
Вписанный угол равен половине градусной меры дуги, на которую
опирается.
На дугу CD опирается вписанный угол САD=60°⇒ она равна 2·60°=120°
На дугу АD опирается вписанный угол АСD=60°⇒ она равна 2·60°=120°
∠А=С=90°
∠В=120°
∠Д=60°
градусные меры дуг
AB=60°
BC=60°
CD=120°
AD=120°.
Объяснение:Дано: ΔABC, ∠C = 90°, AC = 5 CM, BC = 12 CM.
Знайти: sin ∠A, cos ∠A.
Розв’язання. За умовою задано ΔABC, ∠C = 90°, АС = 5 см, ВС = 12 см, тоді За теоремою Піфагора Тоді
Відповідь: 12/13; 5/13.
718. Дано: ΔАВС, ∠C = 90°, АС = 7 см, ВС = 24 см.
Знайти: sin ∠B, cos ∠B.
Розв’язання. За умовою задано ΔABC, ∠С = 90°, АС = 7 см, ВС = 24 см, тоді За теоремою Піфагора АВ2 = ВС2 + АС2. Отже, Тоді
Відповідь: 7/25; 24/25.
719. 1) Дано: ΔАВС, ∠С = 90°, ВС = a, ∠B = β.
Знайти: АС.
Розв’язання. За умовою у ΔАВС ∠C = 90°, ВС = а, ∠В = β. Тоді АС = ВС ∙ tg ∠B; АС = a tg β.
Відповідь: а ∙ tg β.
2) Дано: ΔАВС, ∠С = 90°, АС = b, ∠А = α.
Знайти: АВ.
За умовою у ΔАВС ∠C = 90°, АС = b, ∠A = α. Тоді
Відповідь:
723. 1) Дано: ΔABC, ∠C = 90°, AC = 4√3 CM, ∠A = 30°. Знайти: AB.
2) Дано: ΔABC, ∠C = 90°, AB = 5√2 CM, ∠B = 45°. Знайти: AC.
Розв’язання. За умовою задано ΔABC, ∠C = 90°,
1) Оскільки АС = 4√3 CM, ∠A = 30°, то маємо:
Відповідь: 8 см.
2) Оскільки АВ = 5√2 см, ∠B = 45°, то
Відповідь: 5 см.
724. 1) Дано: ΔАВС, ∠C = 90°, ВС = 6√3 см, АВ = 30°. Знайти: АВ.
2) Дано: ΔABC, ∠C = 90°, АВ = 10√2 см, ∠A = 45°. Знайти: ВС.
Розв’язання. За умовою задано ΔABC, ∠C = 90°.
1) Оскільки ВС = 6√3 CM, ∠B = 30°, то
Відповідь: 12 см.
2) Оскільки АВ = 10√2 см, ∠A = 45°, то
Відповідь: 10 см.
727. 1) Дано: ΔABC, ∠C = 90°, BC = 5 CM, ∠A = 42°. Знайти: AB.
Розв’язання. За умовою у ΔАВС ∠C = 90°, ВС = 5 см, ∠A = 42°. Тоді
Відповідь: 7,48 см.
2) Дано: ΔABC, ∠C = 90°, АВ = 10 см, ∠B = 37°. Знайти: ВС.
Розв'язання. За умовою у ΔАВС ∠C = 90°, АВ = 10 см, ∠B = 37°. Тоді ВС = АВ ∙ cos ∠B, ВС = 10 ∙ cos 37° = 10 ∙ 0,799 = 7,99 см.
Відповідь: 7,99 см.
3) Дано: ΔABC, ∠C = 90°, АС = 4 см, ∠A = 82°. Знайти: ВС.
Розв’язання. За умовою у ΔАВС ∠C = 90°, АС = 4 см, ∠A = 82°. Тоді ВС = АС ∙ tg ∠A; ВС = 4 ∙ tg 82° = 4 ∙ 7,116 = 28,46 см.
Відповідь: 28,46 см.
728. 1) Дано: AABC, ZC = 90°, АВ = 8 см, ZA = 15°. Знайти: АС.
Розв’язання. За умовою у ΔАВС ∠C = 90°, АВ = 8 см, ∠A = 15°, тоді АС = АВ ∙ cos ∠A, АС = 8 ∙ cos 15° = 8 ∙ 0,966 = 7,63 см.
Відповідь: 7,73 см.
2) Дано: ΔABC, ∠C = 90°, ВС = 9 см, ∠A = 43°. Знайти: АВ.
Розв’язання. За умовою у ΔАВС ∠C = 90°, ВС = 9 см, ∠A = 43°, тоді
Відповідь: 13,20 см.
3) Дано: ΔАВС, ∠C = 90°, АС = 5 CM, ∠B = 29°. Знайти: ВС.
Розв’язання. За умовою задано ΔABC, ∠C = 90°, АС = 5 CM, ∠B = 29°, тоді
Відповідь: 9,03 CM.
729. 1) Для того щоб побудувати ∠A, треба:
1. Побудувати прямий кут, ∠C.
2. На одній його стороні відкласти відрізок СА = 5 одиничним відрізкам.
3. На другий стороні прямого кута відкласти відрізок СВ = 3 одиничним відрізкам.
4. З’єднати т. А та т. В.
У прямокутному трикутнику
2) Для того щоб побудувати ∠A, sin ∠A = 1/7, треба:
1. Побудувати прямий кут С.
2. На одній його стороні відкласти відрізок АС = 1 одиничному відрізку.
3. Із точки В, як із центра, радіусом, що дорівнює 7 таким самим одиничним відрізкам, описати дугу до перетину з іншою стороною прямого кута. Точку перетину позначити А. З’єднати т. А і т. В, отримаємо прямокутний трикутник ABC.
Кут А буде шуканим, оскільки sin ∠A = 1/7.
3) Для того щоб побудувати ∠A, cos ∠A = 2/3, треба:
1. Побудувати прямий кут С.
2. На одній з його сторін від вершини відкласти відрізок АС = 2 одиничним відрізкам. .
3. Із точки А, як із центра, радіусом, що дорівнює 3 таким самим одиничним відрізкам, описати дугу до перетину з іншою стороною прямого кута. Позначити точку В.
4. З’єднаємо т. А і т. В, отримаємо прямокутний ΔABC.
∠A — шуканий, оскільки cos ∠A = 2/3.
730. Аналогічно № 729.
731. Дано: ABCD — прямокутник, АС = a, ∠ACB = β.
Знайти: РABCD.