На стороне AB равностороннего треугольника ABC взята точка D так, что сумма расстояний от нее до сторон AC и BC равна 16 см. Найдите высоту треугольника, проведенную из вершины C.
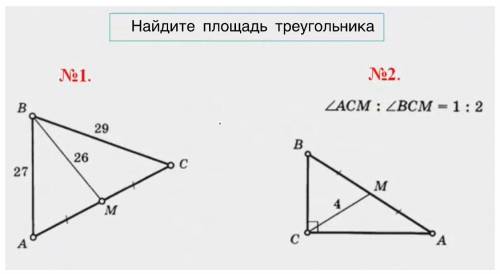
РЕШЕНИЕ: Пусть сторона треугольника а. Одно из данных расстояний m, другое – n. Расстояния – это высоты. Находим площади треугольников:
Сюда относится картинка с умножением
Теперь их суммируем:
Сюда с сложением
В левой части полная площадь ABC, правую можно периписать так:
Сюда с сложением и умножением
Где h - высота из вершины C, равна сумме расстояний = 16 см
ОТВЕТ: 16 см
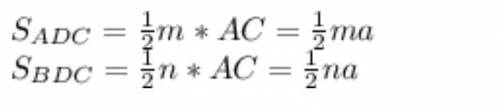
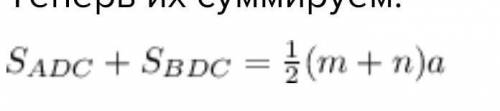
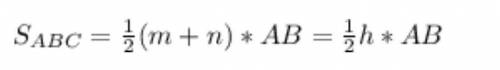
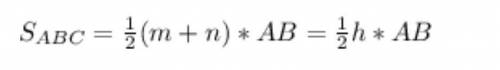
1) Пл.пов.шара = 4pi*r^2=3,5*2
2) Площади имеют квадратичную зависимость, потому, в 81 раз.
3) Очевидно, образующая наклонена под 45 градусов к большей окружности сферы, по совместительству, и основанию конуса (радиус сферы является в данном случае и радиусом основания конуса, и высотой конуса). (12*sqrt(2))^2=2*x^2, x - радиус сферы. X = 12.
4) Основания цилиндра имеют одинаковый размер с большей окружностью сферы. Также, 2*2pi*r^2+2*pi*r*(2r)=36 (так как это площадь цилиндра.
8*pi*r^2=36 => S(сф) = 4*pi*r^2=18
5) Диаметр шара равен трем. Он же равен стороне куба, так как касается противоположных граней куба в точках их центров. Итого, 6*3^2=54.