С=2Πr
r=2S/a+b+c
S=\sqrt{x} p*(p-a)(p-b)(p-c)
p=(a+b+c)/2
p=(4+5+7)/2=8
S=\sqrt{x} 8*(8-4)(8-5)(8-7)=8*4*3*1= 4\sqrt{x}6
r=8\sqrt{x}6/16=\sqrt{x}6/2
C=2\sqrt{x}6/2
C=V6
∠ 1 = ∠ 2 как накрест лежащие углы
Объяснение:
∠ BAC и ∠ DCA образованы при пересечении прямых AB и DC секущей AC. Поэтому ∠ BAC и ∠ DCA - это внутренние накрест лежащие углы.
Если накрест лежащие углы, образующиеся при пересечении двух
прямых секущей, равны, то прямые параллельны.
∠ BAC = ∠ DCA ⇒ AB || DC
∠ 1 и ∠ 2 образованы при пересечении прямых AB и DC секущей BD.
Поэтому ∠ 1 и ∠ 2 - это внутренние накрест лежащие углы.
Так как мы установили, что AB || DC, то ∠ 1 = ∠ 2 (Если две параллельные прямые пересечены секущей, то углы, образующие пару накрест лежащих углов, равны), что и требовалось доказать.
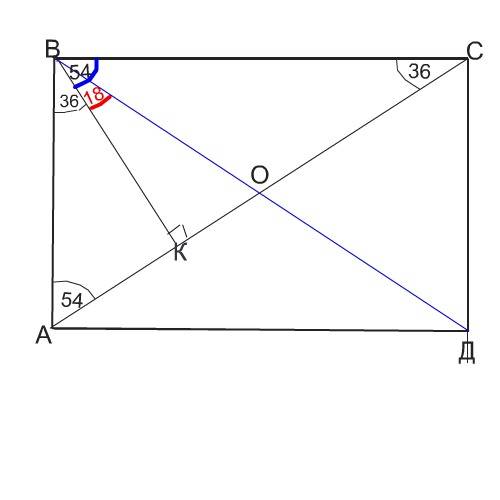
Обозначим для удобства этот прямоугольник АВСД.
Пересечение перпендикуляра из В с диагональю обозначим К.
Если отношение углов, на которые делится прямой угол, равно 2:3, значит, этот угол разделен на 5 частей, 2 из которых принадлежат одному углу, 3 - другому.
90:(2+3)=18°
Угол АВК равен 18*2=36°
Угол СВК равен 18*3=54°
Треугольник ВКС - прямоугольный.
Т.к. угол СВК=54°,
угол ВСА равен 90-54=36°
1) углы, образованные диагоналями со сторонами примоугольника, равны 36° и 54°
---------------------------------------------
Рассматриваем рисунок, чтобы найти ответ на второй вопрос задачи.
Треугоьлник ВОС - равнобедренный по свойству диагоналей прямоугольника, которые равны и точкой пересечения делятся пополам.
Следовательно, угол ОВС равен 36° , а угол КВО, который перпендикуляр КВ образовал с диагональю ВД, равен 54-36=18°
2) ответ на второй вопрос задачи:
Этот угол равен 18°
-------------
Примечание: При решении можно использовать свойство углов при пересечении двух параллельных прямых секущей. Я выбрала решение через треугольники.
r=S/p
S=Vp(p-a)(p-b)( p-c)
p=a+b+c/2
L=2pir
p=4+5+7/2=8
S=V8*4*3*1=V96 = 4V6
r=4V6/8=V6/2
L=2*pi*V6/2=V6pi